
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)证明:函数![]() 在定义域上只有一个零点
在定义域上只有一个零点
【答案】(1)答案见解析;(2)证明见解析.
【解析】
(1)首先求出函数的导函数,令![]() 得
得![]() 或
或![]() ,再对
,再对![]() 分类讨论可得;
分类讨论可得;
(2)由(1)函数的单调性结合零点存在性定理,分类讨论计算可得;
解:(1)![]() ,
,![]() ,
,
令![]() 得
得![]() 或
或![]() ,易知,当
,易知,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
①当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 单调递减;
单调递减;
②当![]() 时,令
时,令![]() 得
得![]() 或
或![]() ,令
,令![]() 得
得![]() ,
,
故![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
③当![]() 时,令
时,令![]() 得
得![]() 或
或![]() ,令
,令![]() 得
得![]() ,
,
故![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
综上,当![]() 时,
时,![]() 在
在![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
(2)由(1)知,①当![]() 时,
时,![]() 在
在![]() 单调递减;
单调递减;
且![]() ,
,
![]() ,即
,即![]() ,故函数
,故函数![]() 在
在![]() 上只有一个零点.
上只有一个零点.
②当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增;故
单调递增;故![]() 的极小值为
的极小值为![]() ,因此
,因此![]() 在
在![]() 上无零点;
上无零点;![]() 的极大值为
的极大值为![]() ,又
,又![]() ,
,![]() ,故
,故![]() 在
在![]() 上有一个零点,因此,函数
上有一个零点,因此,函数![]() 在
在![]() 上只有一个零点.
上只有一个零点.
③当![]() 时,
时,![]() 在
在![]() ,
,![]() 单调递减,在
单调递减,在![]() 单调递增.故
单调递增.故![]() 的极小值为
的极小值为![]() ,又
,又![]() ,
,![]() ,故
,故![]() 在
在![]() 上有一个零点,
上有一个零点,![]() 的极大值为
的极大值为![]() ,又
,又![]() ,故
,故![]() 在
在![]() 上无零点,因此,函数
上无零点,因此,函数![]() 在
在![]() 上只有一个零点.
上只有一个零点.
综上,函数![]() 在
在![]() 上只有一个零点.
上只有一个零点.


科目:高中数学 来源: 题型:
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() ,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
,现有甲,乙二人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球即终止,每个球在每一次被取出的机会是等可能的.
(Ⅰ)求袋中原有白球的个数:
(Ⅱ)求取球次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1000多年,在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵(qian du);阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖膈(bie nao)指四个面均为直角三角形的四面体.如图在堑堵![]() 中,
中,![]() .
.
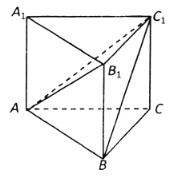
(1)求证:四棱锥![]() 为阳马;
为阳马;
(2)若![]() ,当鳖膈
,当鳖膈![]() 体积最大时,求锐二面角
体积最大时,求锐二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有采购成本分别为![]() 万元/辆和
万元/辆和![]() 万元/辆的
万元/辆的![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:

(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
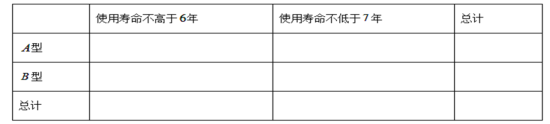
(2)从![]() 和
和![]() 的车型中各随机抽取
的车型中各随机抽取![]() 车,以
车,以![]() 表示这
表示这![]() 车中使用寿命不低于
车中使用寿命不低于![]() 年的车数,求
年的车数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)根据公司要求,采购成本由出租公司负责,平均每辆出租车每年上交公司![]() 万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这
万元,其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年,用频率估计每辆出租车使用寿命的概率,分别以这![]() 辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
辆出租车所产生的平均利润作为决策依据,如果你是该公司的负责人,会选择采购哪款车型?
附: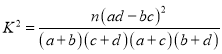 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρsinθ=2.
(1)M为曲线C1上的动点,点P在线段OM上,且满足![]() ,求点P的轨迹C2的直角坐标方程;
,求点P的轨迹C2的直角坐标方程;
(2)曲线C2上两点![]() 与点B(ρ2,α),求△OAB面积的最大值.
与点B(ρ2,α),求△OAB面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线C的极坐标方程;
(2)若直线![]() 与直线l相交于点A,与曲线C相交于不同的两点M,N.求
与直线l相交于点A,与曲线C相交于不同的两点M,N.求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com