
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数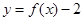 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
(1)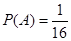 ;(2)
;(2)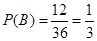 .
.
解析试题分析:(1)根据函数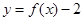 在区间
在区间 上有两个不同的零点,
上有两个不同的零点,
得知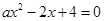 有两个不同的正根
有两个不同的正根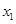 和
和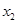 ,
,
由不等式组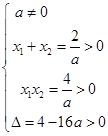
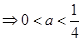 ,利用几何概型得解.
,利用几何概型得解.
(2)应用基本不等式得到 ,
,
由于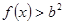 在
在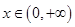 恒成立,得到
恒成立,得到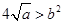 ;
;
讨论当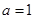 ,
,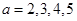 ,
,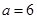 的情况,
的情况,
得到满足条件的基本事件个数,而基本事件总数为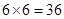 , 故应用古典概型概率的计算公式即得解.
, 故应用古典概型概率的计算公式即得解.
试题解析:(1)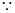 函数
函数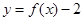 在区间
在区间 上有两个不同的零点,
上有两个不同的零点,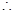
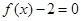 ,即
,即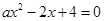 有两个不同的正根
有两个不同的正根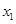 和
和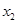
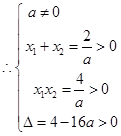
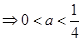 4分
4分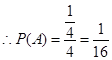 6分
6分
(2)由已知: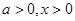 ,所以
,所以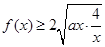 ,即
,即
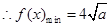 ,
, 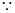
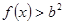 在
在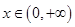 恒成立
恒成立 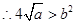
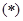 8分
8分
当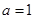 时,
时,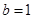 适合
适合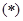 ;
;
当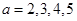 时,
时,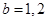 均适合
均适合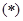 ;
;
当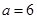 时,
时,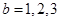 均适合
均适合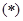 ;
;
满足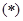 的基本事件个数为
的基本事件个数为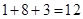 . 10分
. 10分
而基本事件总数为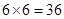 , 11分
, 11分 . 12分
. 12分
考点:古典概型,几何概型,一元二次方程根的分别,基本不等式的应用,不等式恒成立问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(13分)(2011•重庆)某市公租房的房源位于A、B、C三个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,求该市的4位申请人中:
(I)没有人申请A片区房源的概率;
(II)每个片区的房源都有人申请的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学在高一开设了数学史等4门不同的选修课,每个学生必须选修,且只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。
(1)求恰有2门选修课这3个学生都没有选择的概率;
(2)设随机变量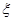 为甲、乙、丙这三个学生选修数学史这门课的人数,求
为甲、乙、丙这三个学生选修数学史这门课的人数,求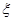 的分布列及期望,方差.
的分布列及期望,方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和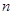 个黑球(
个黑球(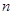 为正整数).现从甲、乙两个盒内各任取2个球,若取出的4个球均为黑球的概率为
为正整数).现从甲、乙两个盒内各任取2个球,若取出的4个球均为黑球的概率为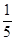 ,求
,求
(1)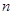 的值;
的值;
(2)取出的4个球中黑球个数大于红球个数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对有 个元素的总体
个元素的总体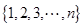 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体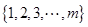 和
和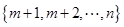 (
(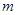 是给定的正整数,且
是给定的正整数,且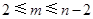 ),再从每个子总体中各随机抽取
),再从每个子总体中各随机抽取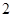 个元素组成样本.用
个元素组成样本.用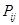 表示元素
表示元素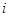 和
和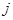 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求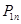 的表达式(用
的表达式(用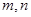 表示);
表示);
(2)求所有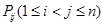 的和.
的和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.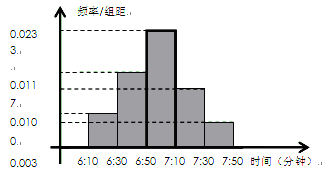
(1)根据图中的数据信息,求出众数 和中位数
和中位数 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间 在上午
在上午 之间,而送报人每天在
之间,而送报人每天在 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件 )的概率.
)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三名射击运动员射中目标的概率分别为 、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.
、a、a(0<a<1),三人各射击一次,击中目标的次数记为ξ.
(1)求ξ的分布列及数学期望;
(2)在概率P(ξ=i)(i=0、1、2、3)中,若P(ξ=1)的值最大,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |  | 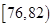 |  |  | 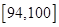 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com