
(13分)已知圆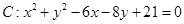 和直线
和直线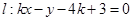 .
.
⑴ 证明:不论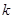 取何值,直线
取何值,直线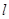 和圆
和圆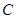 总相交;
总相交;
⑵ 当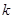 取何值时,圆
取何值时,圆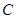 被直线
被直线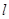 截得的弦长最短?并求最短的弦的长度.
截得的弦长最短?并求最短的弦的长度.
24.⑴. 【证明】
方法一:圆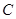 的方程可化为:
的方程可化为: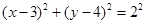 ,圆心为
,圆心为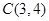 ,半径
,半径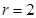 .
.
直线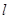 的方程可化为:
的方程可化为: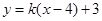 ,直线过定点
,直线过定点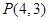 ,斜率为
,斜率为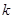 .
.
定点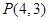 到圆心
到圆心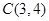 的距离
的距离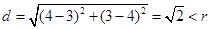 ,
,
∴定点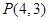 在圆
在圆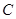 内部,∴不论
内部,∴不论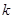 取何值,直线
取何值,直线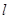 和圆
和圆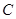 总相交.
总相交.
方法二:圆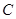 的方程可化为:
的方程可化为: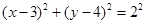 ,圆心为
,圆心为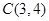 ,半径
,半径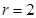 .
.
圆心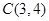 到直线
到直线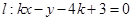 的距离
的距离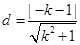 ,
,
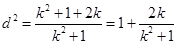 ,因
,因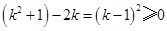 ,
,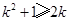 ,
,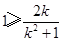 ,
,
故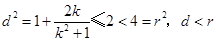 ,∴不论
,∴不论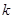 取何值,直线
取何值,直线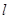 和圆
和圆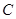 总相交.
总相交.
⑵. 圆心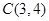 到直线
到直线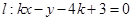 的距离
的距离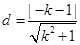
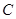 被直线
被直线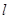 截得的弦长=
截得的弦长=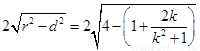 ,
,
当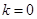 时,弦长
时,弦长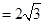 ;
;
当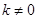 时,弦长
时,弦长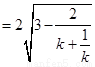 ,下面考虑先求函数
,下面考虑先求函数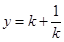 的值域.
的值域.
由函数知识可以证明:函数在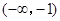 上单调递增,在
上单调递增,在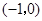 上单调递减,在
上单调递减,在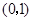 上单调递减,在
上单调递减,在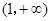 上单调递增(证明略),
上单调递增(证明略),
故当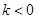 时,函数在
时,函数在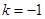 处取得最大值-2;当
处取得最大值-2;当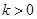 时,函数在
时,函数在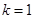 处取得最小值2.
处取得最小值2.
即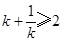 或
或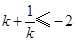 ,
,
故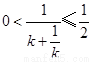 或
或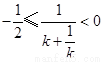 ,可得
,可得
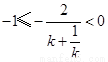 或
或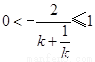 ,即
,即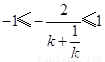 且
且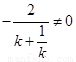 ,
,
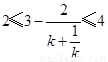 且
且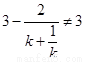 ,
,
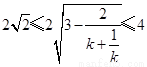 且
且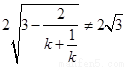 .
.
综上,当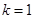 时,弦长取得最小值
时,弦长取得最小值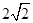 ;当
;当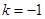 时,弦长取得最大值4.
时,弦长取得最大值4.
【解析】略


科目:高中数学 来源:2014届四川省高二10月月考文科数学试卷(解析版) 题型:解答题
已知圆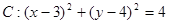 和直线
和直线
(1) 求证:不论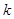 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;
(2) 求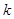 取何值时,圆被直线截得的弦最短,并求最短弦的长.
取何值时,圆被直线截得的弦最短,并求最短弦的长.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三高考压轴数学试卷(解析版) 题型:解答题
在极坐标系下,已知圆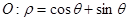 和直线
和直线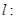
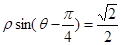 .
.
(1)求圆 和直线
和直线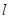 的直角坐标方程;
的直角坐标方程;
(2)当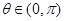 时,求直线
时,求直线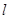 与圆
与圆 公共点的极坐标.
公共点的极坐标.
查看答案和解析>>
科目:高中数学 来源:2013届北京市高二上学期期中考试数学试卷 题型:解答题
已知圆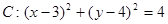 和直线
和直线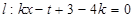 ,
,
(1)求证:不论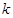 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;
(2)求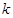 取何值时,直线被圆截得的弦最短,并求出最短弦的长;
取何值时,直线被圆截得的弦最短,并求出最短弦的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com