
【题目】设函数![]()
,曲线![]()
过点![]()
,且在点![]()
处的切线方程为![]()
.
(1)求![]()
的值;
(2)证明:当![]()
时, ![]()
;
(3)若当![]()
时, ![]()
恒成立,求实数![]()
的取值范围.
【答案】(1)![]()
;(2)详见解析;(3)![]()
.
【解析】试题分析:(1)根据导数几何意义得![]()
,再结合![]()
联立方程组,解得![]()
的值;(2)即证明差函数![]()
的最小值非负,先求差函数的导数,为研究导函数符号,需对导函数再次求导,得导函数最小值为零,因此差函数单调递增,也即差函数最小值为![]()
,(3)不等式恒成立问题,一般转化为对应函数最值问题,本题仍研究差函数![]()
,因为![]()
,所以![]()
.先求差函数导数,再求导函数的导数得![]()
,所以分![]()
进行讨论:当![]()
时, ![]()
满足题意;当![]()
时,能找到一个减区间,使得![]()
不满足题意.
试题解析:(1)由题意可知, ![]()
定义域为![]()
![]()
,
![]()
, ![]()
![]()
.
(2)![]()
,
设![]()
, ![]()
, ![]()
由![]()
,![]()
![]()
在![]()
上单调递增,
∴![]()
,![]()
![]()
在![]()
上单调递增,![]()
![]()
.
∴![]()
.
(3)设![]()
, ![]()
, ![]()
,
由(2)中知![]()
,![]()
![]()
,
∴![]()
,
当![]()
即![]()
时, ![]()
,
所以![]()
在![]()
单调递增, ![]()
,成立.
②当![]()
即![]()
时, ![]()
![]()
,令
,得![]()
,
当![]()
时, ![]()
单调递减,则![]()
,
所以![]()
在![]()
上单调递减,所以![]()
,不成立.
综上, ![]()
.


科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.命题“p且q”为真,则![]() 恰有一个为真命题
恰有一个为真命题
B.命题“已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件”
”的充分不必要条件”
C.命题![]() 都有
都有![]() ,则
,则![]() ,使得
,使得![]()
D.如果函数![]() 在区间
在区间![]() 上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有![]() ,那么函数
,那么函数![]() 在区间
在区间![]() 内有零点
内有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生220人,学籍编号为1,2,…,220;女生380人,学籍编号为221,222,…,600.为了解学生学习的心理状态,按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为10),再从这10名学生中随机抽取3人进行座谈,则这3人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用一个半径为12厘米圆心角为![]() 的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
的扇形纸片PAD卷成一个侧面积最大的无底圆锥(接口不用考虑损失),放于水平面上.
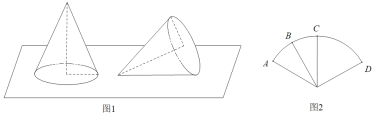
(1)无底圆锥被一阵风吹倒后(如图1),求它的最高点到水平面的距离;
(2)扇形纸片PAD上(如图2),C是弧AD的中点,B是弧AC的中点,卷成无底圆锥后,求异面直线PA与BC所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰好有一个元素,求实数
的解集中恰好有一个元素,求实数![]() 的值;
的值;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过
上的最大值与最小值的差不超过![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com