【题目】已知球的半径为4，球面被互相垂直的两个平面所截，得到的两个圆的公共弦长为2
．若球心到这两个平面的距离相等，则这两个圆的半径之和为（ ）
A. 4B. 6C. 8D. 10
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，曲线
的参数方程为
（
为参数），以原点
为极点，以
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
，
.
（1）当
时，判断曲线与曲线的位置关系；
（2）当曲线上有且只有一点到曲线的距离等于
时，求曲线上到曲线距离为
的点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在四棱锥
中，
平面
，
， 
是线段
的中垂线，
，
为线段
上的点．
（Ⅰ）证明：平面
平面
；
（Ⅱ）若为的中点，求异面直线
与
所成角的正切值；
（Ⅲ）求直线与平面
所成角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市食品药品监督管理局开展2019年春季校园餐饮安全检查，对本市的8所中学食堂进行了原料采购加工标准和卫生标准的检查和评分，其评分情况如下表所示：
中学编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
原料采购加工标准评分x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
卫生标准评分y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
（1）已知x与y之间具有线性相关关系，求y关于x的线性回归方程；（精确到0.1）
（2）现从8个被检查的中学食堂中任意抽取两个组成一组，若两个中学食堂的原料采购加工标准和卫生标准的评分均超过80分，则组成“对比标兵食堂”，求该组被评为“对比标兵食堂”的概率.
参考公式：
，
；
参考数据：
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在矩形
中，
，
，
为边
的中点．将△
沿
翻折，得到四棱锥
．设线段
的中点为
，在翻折过程中，有下列三个命题：
① 总有
平面
；
② 三棱锥
体积的最大值为
；
③ 存在某个位置，使与所成的角为
．
其中正确的命题是____．（写出所有正确命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校为增加应届毕业生就业机会，每年根据应届毕业生的综合素质和学业成绩对学生进行综合评估，已知某年度参与评估的毕业生共有2000名，其评估成绩
近似的服从正态分布
．现随机抽取了100名毕业生的评估成绩作为样本，并把样本数据进行了分组，绘制了频率分布直方图：
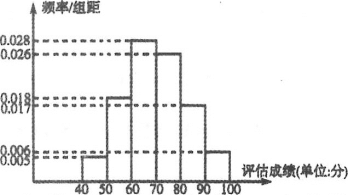
（1）求样本平均数
和样本方差
（同一组中的数据用该组区间的中点值作代表）；
（2）若学校规定评估成绩超过
分的毕业生可参加
三家公司的面试．
（ⅰ）用样本平均数作为
的估计值
，用样本标准差
作为
的估计值
，请利用估计值判断这2000名毕业生中，能够参加三家公司面试的人数；
（ⅱ）若三家公司每家都提供甲、乙、丙三个岗位，岗位工资表如下：
公司 | 甲岗位 | 乙岗位 | 丙岗位 |
| 9600 | 6400 | 5200 |
| 9800 | 7200 | 5400 |
| 10000 | 6000 | 5000 |
李华同学取得了三个公司的面试机会，经过评估，李华在三个公司甲、乙、丙三个岗位的面试成功的概率均为
,李华准备依次从三家公司进行面试选岗，公司规定：面试成功必须当场选岗，且只有一次机会．李华在某公司选岗时，若以该岗位工资与未进行面试公司的工资期望作为抉择依据，问李华可以选择公司的哪些岗位？
并说明理由．
附：
，若随机变量
，
则
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
