
【题目】定义域为集合![]() 上的函数
上的函数![]() 满足:①
满足:①![]() ;②
;②![]() (
(![]() );③
);③![]() 、
、![]() 、
、![]() 成等比数列;这样的不同函数
成等比数列;这样的不同函数![]() 的个数为________
的个数为________
【答案】![]()
【解析】
分析出f(x)的所有可能的取值,得到使f(x)中f(1)、f(6)、f(12)成等比数列时对应的项,再运用计数原理求出这样的不同函数f(x)的个数即可.
解:经分析,f(x)的取值的最大值为x,最小值为2﹣x,并且成以2为公差的等差数列,故f(6)的取值为6,4,2,0,﹣2,﹣4.
f(12)的取值为12,10,8,6,4,2,0,﹣2,﹣4,﹣6,﹣8,﹣10,
所以能使f(x)中的f(1)、f(6)、f(12)成等比数列时,f(1)、f(6)、f(12)的取值只有两种情况:
①f(1)=1、f(6)=2、f(12)=4;②f(1)=1、f(6)=﹣2、f(12)=4.
|f(x+1)﹣f(x)|=1(x=1,2,…,11),f(x+1)=f(x)+1,或者f(x+1)=f(x)﹣1,即得到后项时,把前项加1或者把前项减1.
(1)当f(1)=1、f(6)=2、f(12)=4时;将要构造满足条件的等比数列分为两步,第一步:从f(1)变化到f(6),第二步:从f(6)变化的f(12).
从f(1)变化到f(6)时有5次变化,函数值从1变化到2,故应从5次中选择3步加1,剩余的两次减1.对应的方法数为![]() 10种.
10种.
从f(6)变化到f(12)时有6次变化,函数值从2变化到4,故应从6次变化中选择4次增加1,剩余两次减少1,对应的方法数为![]() 15种.
15种.
根据分步乘法原理,共有10×15=150种方法.
(2)当f(1)=1、f(6)=﹣2、f(12)=4时,将要构造满足条件的等比数列分为两步,第一步:从f(1)变化到f(6),第二步:从f(6)变化的f(12).
从f(1)变化到f(6)时有5次变化,函数值从1变化到﹣2,故应从5次中选择1步加1,剩余的4次减1.对应的方法数为![]() 5种.
5种.
从f(6)变化到f(12)时有6次变化,函数值从﹣2变化到4,故应从6次变化中选择6次增加1,对应的方法数为![]() 1种.
1种.
根据分步乘法原理,共有5×1=5种方法.
综上,满足条件的f(x)共有:150+5=155种.
故填:155.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天,这五家“农家乐的收费标准互不相同得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
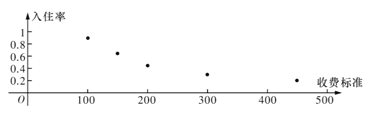
(1)若从以上五家“农家乐”中随机抽取两家深人调查,记![]() 为“入住率超过0.6的农家乐的个数,求
为“入住率超过0.6的农家乐的个数,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,
哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,![]() 的结果精确到0.1)
的结果精确到0.1)
(3)根据第(2)问所求的回归方程,试估计收费标准为多少时,100天销售额L最大?(100天销售额L=100×入住率×收费标准x)
参考数据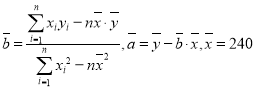 ,
,![]() ,
,![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,直线
,直线![]() 与椭圆C交于A,B两点,且
与椭圆C交于A,B两点,且![]() .
.
(1)求椭圆C的方程.
(2)不经过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长与椭圆C的长轴长相等,且直线
截得的弦长与椭圆C的长轴长相等,且直线![]() 与椭圆C交于D,E两点,试判断
与椭圆C交于D,E两点,试判断![]() 的周长是否为定值?若是,求出定值;若不是,请说明理由.
的周长是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右两焦点分别为
的左右两焦点分别为![]() 、
、![]() .
.
(1)若矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 均在
均在![]() 上,求该矩形绕
上,求该矩形绕![]() 轴旋转一周所得圆柱侧面积
轴旋转一周所得圆柱侧面积![]() 的取值范围;
的取值范围;
(2)设斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() (
(![]() ),求证:
),求证:![]() ;
;
(3)过![]() 上一动点
上一动点![]() 作直线
作直线![]() ,其中
,其中![]() ,过
,过![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,若
,若![]() ,则对此不等式描叙正
,则对此不等式描叙正
确的是( )
A. 若![]() ,则至少存在一个以
,则至少存在一个以![]() 为边长的等边三角形
为边长的等边三角形
B. 若![]() ,则对任意满足不等式的
,则对任意满足不等式的![]() 都存在以
都存在以![]() 为边长的三角形
为边长的三角形
C. 若![]() ,则对任意满足不等式的
,则对任意满足不等式的![]() 都存在以
都存在以![]() 为边长的三角形
为边长的三角形
D. 若![]() ,则对满足不等式的
,则对满足不等式的![]() 不存在以
不存在以![]() 为边长的直角三角形
为边长的直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为一正方体的平面展开图,在这个正方体中,有以下结论:①![]() ,②CF与EN所成的角为
,②CF与EN所成的角为![]() ,③
,③![]() //MN ,④二面角
//MN ,④二面角![]() 的大小为
的大小为![]() ,其中正确的个数是( )
,其中正确的个数是( )
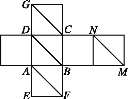
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com