
【题目】已知椭圆![]() 的左右两焦点分别为
的左右两焦点分别为![]() 、
、![]() .
.
(1)若矩形![]() 的边
的边![]() 在
在![]() 轴上,点
轴上,点![]() 、
、![]() 均在
均在![]() 上,求该矩形绕
上,求该矩形绕![]() 轴旋转一周所得圆柱侧面积
轴旋转一周所得圆柱侧面积![]() 的取值范围;
的取值范围;
(2)设斜率为![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() (
(![]() ),求证:
),求证:![]() ;
;
(3)过![]() 上一动点
上一动点![]() 作直线
作直线![]() ,其中
,其中![]() ,过
,过![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,问是否存在实数
,问是否存在实数![]() ,使得
,使得![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)![]() ;(2)见解析;(3)1.
;(2)见解析;(3)1.
【解析】
(1)设D(x,y),由D在椭圆![]() 上,可得|xy|
上,可得|xy|![]() ,再由矩形绕y轴旋转一周后所得圆柱体侧面积为S侧=2π|BC||AB|=4π|xy|求解;
,再由矩形绕y轴旋转一周后所得圆柱体侧面积为S侧=2π|BC||AB|=4π|xy|求解;
(2)设P(x1,y1),Q(x2,y2),利用点差法可得k![]()
![]() ,再由M(1,m)在椭圆内部,得m2
,再由M(1,m)在椭圆内部,得m2![]() ,即0<m
,即0<m![]() ,由此证明结论;
,由此证明结论;
(3)直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,求出
,求出![]() ,
,![]() ,再由到角公式可得ER为∠F1EF2的角分线,得到
,再由到角公式可得ER为∠F1EF2的角分线,得到![]() ,即|EF1||RF2|=λ|EF2||RF1|,可知存在实数λ=1,使得|EF1||RF2|=λ|EF2||RF1|恒成立.
,即|EF1||RF2|=λ|EF2||RF1|,可知存在实数λ=1,使得|EF1||RF2|=λ|EF2||RF1|恒成立.
(1)解:设D(x,y),由D在椭圆![]() 上,
上,
得1![]() ,得|xy|
,得|xy|![]() ,
,
当且仅当![]() ,即
,即![]() ,
,![]() 时取“=”.
时取“=”.
矩形绕y轴旋转一周后所得圆柱体侧面积为S侧=2π|BC|AB|=4π|xy|,
∴S侧=4π|xy|≤4![]() π;
π;
(2)证明:设P(x1,y1),Q(x2,y2),
则![]() ,
,![]() ,
,
两式作差可得:k![]()
![]() ,
,
由M(1,m)在椭圆内部,得![]() ,即m2
,即m2![]() ,
,
又m>0,∴0<m![]() ,得k
,得k![]() ;
;
(3)解:直线![]() 的斜率为
的斜率为![]() ,则
,则![]() ,
,
又![]() ,
,![]() ,
,
设直线EF1到直线ER的角为α,直线ER到直线EF2的角为β,
则tanα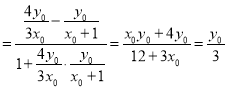 ,
,
tanβ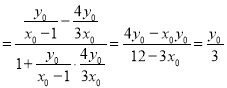 .
.
∴tanα=tanβ,则α=β,即ER为∠F1EF2的角分线,
∴![]() ,即|EF1||RF2|=λ|EF2||RF1|,
,即|EF1||RF2|=λ|EF2||RF1|,
∴存在实数λ=1,使得|EF1||RF2|=λ|EF2||RF1|恒成立.


科目:高中数学 来源: 题型:
【题目】过抛物线y2=4x焦点F的直线交抛物线于A、B两点,交其准线于点C,且A、C位于x轴同侧,若|AC|=2|AF|,则|BF|等于( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生成的产品生产线上随机抽取![]() 件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
件产品,测量这批产品的一项质量指标值,由测量结果得如图所示的频率分布直方图:
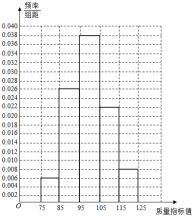
(1)估计这批产品质量指标值的样本平均![]() 和样本方差
和样本方差![]() (同一组中的数据用该组区间的中点值做代表):
(同一组中的数据用该组区间的中点值做代表):
(2)若该种产品的等级及相应等级产品的利润(每件)参照以下规则(其中![]() 为产品质量指标值):当
为产品质量指标值):当![]() 该产品定为一等品,企业可获利
该产品定为一等品,企业可获利![]() 元;当
元;当![]() 且
且![]() 该产品定为二等品,企业可获利
该产品定为二等品,企业可获利![]() 元:当
元:当![]() 且
且![]() .该产品定为三等品,企业将损失
.该产品定为三等品,企业将损失![]() 元;否则该产品定为不合格品,企业将损失
元;否则该产品定为不合格品,企业将损失![]() 元
元
(i)若测得一箱产品(![]() 件)的质量指标数据分别为:
件)的质量指标数据分别为:![]() ,求该箱产品的利润;
,求该箱产品的利润;
(ii)设事件![]() ;事件
;事件![]() 事件
事件![]() 根据经验,对于该生产线上的产品,事件
根据经验,对于该生产线上的产品,事件![]() 发生的概率分别为
发生的概率分别为![]() ,根据以上信息,若产品预计年产量为
,根据以上信息,若产品预计年产量为![]() 件,试估计设产品年获利情况(参考数据:
件,试估计设产品年获利情况(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车是我国汽车工业由大变强的一条必经之路!国家对其给予政策上的扶持,己成为我国的战略方针.近年来,我国新能源汽车制造蓬勃发展,某著名车企自主创新,研发了一款新能源汽车,经过大数据分析获得:在某种路面上,该品牌汽车的刹车距离![]() (米)与其车速
(米)与其车速![]() (千米/小时)满足下列关系:
(千米/小时)满足下列关系:![]() (
(![]() ,
,![]() 是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离
是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离![]() (米)与该车的车速
(米)与该车的车速![]() (千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为
(千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为![]() ,在乙地的销售利润(单位:万元)为
,在乙地的销售利润(单位:万元)为![]() ,其中
,其中![]() 为销售量(单位:辆).
为销售量(单位:辆).
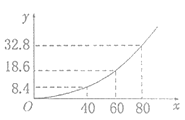
(1)若该公司在两地共销售20辆该品牌的新能源汽车,则能获得的最大利润![]() 是多少?
是多少?
(2)如果要求刹车距离不超过25.2米,求该品牌新能源汽车行驶的最大速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com