
【题目】对于定义域为![]() 的函数
的函数![]() ,如果同时满足以下三个条件:①任意的
,如果同时满足以下三个条件:①任意的![]() ,总有
,总有![]() ;②
;②![]() ;③若
;③若![]() ,
,![]() ,
,![]() ,总有
,总有![]() 成立,则称函数
成立,则称函数![]() 为理想函数.
为理想函数.
(1)证明:若函数![]() 为理想函数,则
为理想函数,则![]() ;
;
(2)证明:函数![]() ,
,![]() 是理想函数;
是理想函数;
(3)证明:若函数![]() 为理想函数,假定存在
为理想函数,假定存在![]() ,使得
,使得![]() 且
且![]() ,则
,则![]() .
.
科目:高中数学 来源: 题型:
【题目】某工厂生产一批零件,为了解这批零件的质量状况,检验员从这批产品中随机抽取了100件作为样本进行检测,将它们的重量(单位:g)作为质量指标值,由检测结果得到如下频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
| 8 | |
| ||
| ||
| 16 | 0.16 |
| 4 | 0.04 |
合计 | 100 | 1 |
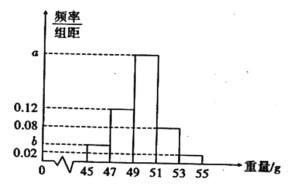
(1)求图中![]() ,
,![]() 的值;
的值;
(2)根据质量标准规定:零件重量小于47或大于53为不合格品,重量在区间![]() 和
和![]() 内为合格品,重量在区间
内为合格品,重量在区间![]() 内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
内为优质品.已知每件产品的检测费用为5元,每件不合格品的回收处理费用为20元.以抽检样本重量的频率分布作为该批零件重量的概率分布.若这批零件共400件,现有两种销售方案:
方案一:对剩余零件不再进行检测,回收处理这100件样本中的不合格品,余下所有零件均按150元/件售出;
方案二:继续对剩余零件的重量进行逐一检测,回收处理所有不合格品,合格品按150元/件售出,优质品按200元/件售出.
仅从获得利润大的角度考虑,该生产商应选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究机构为了解某学校学生使用手机的情况,在该校随机抽取了60名学生(其中男、女生人数之比为2:1)进行问卷调查.进行统计后将这60名学生按男、女分为两组,再将每组学生每天使用手机的时间(单位:分钟)分为![]() 5组,得到如图所示的频率分布直方图(所抽取的学生每天使用手机的时间均不超过50分钟).
5组,得到如图所示的频率分布直方图(所抽取的学生每天使用手机的时间均不超过50分钟).
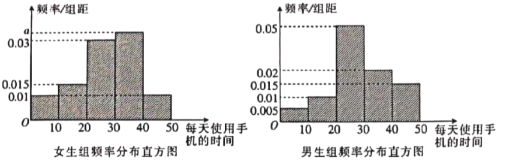
(1)求出女生组频率分布直方图中![]() 的值;
的值;
(2)求抽取的60名学生中每天使用手机时间不少于30分钟的学生人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,丙所得为( )
A.![]() 钱B.1钱C.
钱B.1钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() ,
,![]() 及函数
及函数![]() (
(![]() ),
),![]() (
(![]() ).
).
(1)若等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 的前
的前![]() (
(![]() )项和;
)项和;
(2)已知等差数列![]() 满足
满足![]() ,
,![]() ,
,![]() (
(![]() 、
、![]() 均为常数,
均为常数,![]() ,且
,且![]() ),
),![]() (
(![]() ).试求实数对(
).试求实数对(![]() ,
,![]() ),使得
),使得![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+![]() t≤t2,求实数t的取值范围.
t≤t2,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为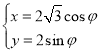 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com