
【题目】平面直角坐标系中,动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,记圆心
相切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设过定点![]() (
(![]() 为非零常数)的动直线
为非零常数)的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,问:在曲线
两点,问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值.若存在,求出点
的斜率之和为定值.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】【试题分析】(1)依据题设条件运用两圆位置关系建立方程求解;(2)依据题设条件借助直线的斜率公式及直线与抛物线的位置关系进行分析求解:
(1)不妨设动圆![]() 的圆心为
的圆心为![]() ,
,
易知圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
∵动圆![]() 与圆
与圆![]() 外切,且与直线
外切,且与直线![]() 相切,
相切,
∴圆心![]() 在直线
在直线![]() 的右侧,且点
的右侧,且点![]() 到点
到点![]() 的距离比点
的距离比点![]() 到直线
到直线![]() 的距离大
的距离大![]() ,
,
即![]() ,且
,且![]() ,
,
∴![]() ,两边平方并化简整理得
,两边平方并化简整理得![]() ,
,
即曲线![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)假设在曲线![]() 上存在点
上存在点![]() 满足题设条件,不妨设
满足题设条件,不妨设![]() ,
,
则![]() ,
,
∴![]() (*)
(*)
显然动直线![]() 的斜率非零,故可设其方程为
的斜率非零,故可设其方程为![]() ,
,
联立![]() ,整理得
,整理得![]() ,
,
∴![]() ,且
,且![]() ,
,
代入(*)式得![]() ,
,
显然![]() ,于是
,于是![]() (**),
(**),
欲使(**)式对任意![]() 成立,∴
成立,∴ ,
,
显然![]() ,否则由
,否则由![]() 可知
可知![]() ,
,
从而可得![]() ,这与
,这与![]() 为非零常数矛盾,
为非零常数矛盾,
∴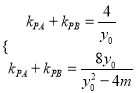 ,
,
∴![]() ,∴
,∴![]() ,
,
于是,当![]() 时,不存在满足条件的
时,不存在满足条件的![]() ,即不存在满足题设条件的点
,即不存在满足题设条件的点![]() ;
;
当![]() 时,
时, ![]() ,
,
将此代入抛物线![]() 的方程可求得满足条件的
的方程可求得满足条件的![]() 点坐标为
点坐标为![]() 或
或![]() .
.
下面说明此时直线![]() 的斜率必定存在,
的斜率必定存在,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
显然![]() ,∴
,∴![]() ,且
,且![]() ,∴直线
,∴直线![]() 的斜率必定存在,
的斜率必定存在,
综上所述,存在点![]() (与
(与![]() 两点相异),其坐标为
两点相异),其坐标为![]() ,或
,或![]() ,使得直线
,使得直线![]() 的斜率之和为定值.
的斜率之和为定值.


科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,且对任意正整数n,点(
,且对任意正整数n,点(![]() ,
,![]() )在直线
)在直线![]() 上.
上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数λ,使得数列{![]() }为等差数列?若存在,求出λ的值;若不存在,请说明理由;
}为等差数列?若存在,求出λ的值;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在(0, ![]() )内,sinx>cosx
)内,sinx>cosx
B.函数y=2sin(x+ ![]() )的图象的一条对称轴是x=
)的图象的一条对称轴是x= ![]() π
π
C.函数y= ![]() 的最大值为π
的最大值为π
D.函数y=sin2x的图象可以由函数y=sin(2x﹣ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),以坐标原点为极点,
),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)讨论直线![]() 与圆
与圆![]() 的公共点个数;
的公共点个数;
(Ⅱ)过极点作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,求点
,求点![]() 的轨迹与圆
的轨迹与圆![]() 相交所得弦长.
相交所得弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据环境保护部《环境空气质量指数(![]() )技术规定》,空气质量指数(
)技术规定》,空气质量指数(![]() )在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
)在201—300之间为重度污染;在301—500之间为严重污染.依据空气质量预报,同时综合考虑空气污染程度和持续时间,将空气重污染分4个预警级别,由轻到重依次为预警四级、预警三级、预警二级、预警一级,分别用蓝、黄、橙、红颜色标示,预警一级(红色)为最高级别.(一)预警四级(蓝色):预测未来1天出现重度污染;(二)预警三级(黄色):预测未来1天出现严重污染或持续3天出现重度污染;(三)预警二级(橙色);预测未来持续3天交替出现重度污染或严重污染;(四)预警一级(红色);预测未来持续3天出现严重污染.
某城市空气质量监测部门对近300天空气中![]() 浓度进行统计,得出这300天
浓度进行统计,得出这300天![]() 浓度的频率分布直方图如图,将
浓度的频率分布直方图如图,将![]() 浓度落入各组的频率视为概率,并假设每天的
浓度落入各组的频率视为概率,并假设每天的![]() 浓度相互独立.
浓度相互独立.
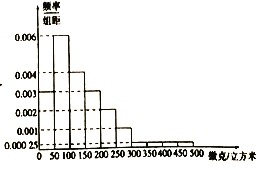
(1)求当地监测部门发布颜色预警的概率;
(2)据当地监测站数据显示未来4天将出现3天严重污染,求监测部门发布红色预警的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com