
【题目】设有三个乡镇,分别位于一个矩形![]() 的两个顶点M,N及
的两个顶点M,N及![]() 的中点S处,
的中点S处,![]() ,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为
,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为![]() .
.
(1)设![]() ,试将L表示为x的函数并写出其定义域;
,试将L表示为x的函数并写出其定义域;
(2)试利用(1)的函数关系式确定宣讲站O的位置,使宣讲站O到三个乡镇的距离之和![]() 最小.
最小.
科目:高中数学 来源: 题型:
【题目】太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼,它形象化的表达了阴阳轮转,相反相成是万物生成变化根源的哲理,展现了一种相互转化,相对统一的形式美.如图,按照太极图的构图方法,在平面直角坐标系中,圆![]() 被函数
被函数![]() 的图象分割为两个对称的鱼形图案,其中两个小圆的周长均为
的图象分割为两个对称的鱼形图案,其中两个小圆的周长均为![]() ,现在大圆内随机取一点,则此点取自阴影部分的概率为( )
,现在大圆内随机取一点,则此点取自阴影部分的概率为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】西北某省会城市计划新修一座城市运动公园,设计平面如图所示:其为五边形![]() ,其中三角形区域
,其中三角形区域![]() 为球类活动场所;四边形
为球类活动场所;四边形![]() 为文艺活动场所,
为文艺活动场所,![]() ,为运动小道(不考虑宽度)
,为运动小道(不考虑宽度)![]() ,
,![]() ,
,![]() 千米.
千米.
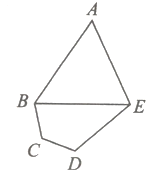
(1)求小道![]() 的长度;
的长度;
(2)求球类活动场所![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A、B、C、D为空间四个不共面的点,以![]() 的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
的概率在每对点之间连一条边,任意两对点之间是否连边是相互独立的,则点A与B可用(一条边或者若干条边组成的)空间折线连接的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为偶函数.
为偶函数.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若函数![]() ,
,![]() ,是否存在实数m,使得
,是否存在实数m,使得![]() 的最小值为2,若存在,请求出m的值;若不存在,请说明理由.
的最小值为2,若存在,请求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气![]() 后,测得车库内的一氧化碳浓度为
后,测得车库内的一氧化碳浓度为![]() ,继续排气
,继续排气![]() ,又测得浓度为
,又测得浓度为![]() ,经检测知该地下车库一氧化碳浓度
,经检测知该地下车库一氧化碳浓度![]() 与排气时间
与排气时间![]() 存在函数关系:
存在函数关系: (
(![]() ,
,![]() 为常数)。
为常数)。
(1)求![]() ,
,![]() 的值;
的值;
(2)若地下车库中一氧化碳浓度不高于![]() 为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com