
【题目】某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳含量达到了危险状态,经抢修,排气扇恢复正常.排气![]() 后,测得车库内的一氧化碳浓度为
后,测得车库内的一氧化碳浓度为![]() ,继续排气
,继续排气![]() ,又测得浓度为
,又测得浓度为![]() ,经检测知该地下车库一氧化碳浓度
,经检测知该地下车库一氧化碳浓度![]() 与排气时间
与排气时间![]() 存在函数关系:
存在函数关系: (
(![]() ,
,![]() 为常数)。
为常数)。
(1)求![]() ,
,![]() 的值;
的值;
(2)若地下车库中一氧化碳浓度不高于![]() 为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
为正常,问至少排气多少分钟,这个地下车库中的一氧化碳含量才能达到正常状态?
科目:高中数学 来源: 题型:
【题目】如图,O为坐标原点,点F为抛物线C1:![]() 的焦点,且抛物线C1上点P处的切线与圆C2:
的焦点,且抛物线C1上点P处的切线与圆C2:![]() 相切于点Q.
相切于点Q.

(Ⅰ)当直线PQ的方程为![]() 时,求 抛物线C1的方程;
时,求 抛物线C1的方程;
(Ⅱ)当正数P变化时,记S1 ,S2分别为△FPQ,△FOQ的面积,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有三个乡镇,分别位于一个矩形![]() 的两个顶点M,N及
的两个顶点M,N及![]() 的中点S处,
的中点S处,![]() ,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为
,现要在该矩形的区域内(含边界),且与M,N等距离的一点O处设一个宣讲站,记O点到三个乡镇的距离之和为![]() .
.
(1)设![]() ,试将L表示为x的函数并写出其定义域;
,试将L表示为x的函数并写出其定义域;
(2)试利用(1)的函数关系式确定宣讲站O的位置,使宣讲站O到三个乡镇的距离之和![]() 最小.
最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,且
,且![]() ).
).
(1)当![]() (其中
(其中![]() ,且t为常数)时,
,且t为常数)时,![]() 是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由;
是否存在最小值,如果存在,求出最小值;如果不存在,请说明理由;
(2)当![]() 时,求满足不等式
时,求满足不等式![]() 的实数x的取值范围.
的实数x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,函数
,函数![]() 的图象在
的图象在![]() 处的切线与直线
处的切线与直线![]() 平行.
平行.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)若函数![]() 存在单调递减区间,求实数
存在单调递减区间,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() (
(![]() )是函数
)是函数![]() 的两个极值点,若
的两个极值点,若![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
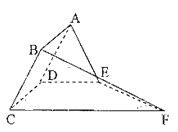
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .若存在,请求出
.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com