
【题目】设函数![]() ,
, ![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 处取得极大值,求正实数
处取得极大值,求正实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)正实数![]() 的取值范围为
的取值范围为![]() 。
。
【解析】试题分析:(1)求出![]() ,分两种情况讨论,分别令
,分两种情况讨论,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)讨论
的减区间;(2)讨论![]() 的取值范围,分别利用导数研究函数的单调性,根据函数极值的定义,进行验证即可得到结论.
的取值范围,分别利用导数研究函数的单调性,根据函数极值的定义,进行验证即可得到结论.
试题解析:(1)由![]() ,
,
所以![]() .
.
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,
单调递增, ![]() 时,
时, ![]() ,函数
,函数![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)∵![]() ,
,
∴![]() 且
且![]() .
.
由(1)知①当![]() 时,
时, ![]() ,由(1)知
,由(1)知![]() 在
在![]() 内单调递增,可得当
内单调递增,可得当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,所以
内单调递增,所以![]() 在
在![]() 处取得极小值,不合题意.
处取得极小值,不合题意.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,所以当
内单调递减,所以当![]() 时,
时, ![]() ,
, ![]() 单调递减,不合题意.
单调递减,不合题意.
③当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
所以![]() 在
在![]() 处取得极大值,符合题意.
处取得极大值,符合题意.
综上可知,正实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据《中华人民共和国道路交通安全法》规定:“车辆驾驶员血液酒精溶度(单位mg/100ml)/在![]() ,属于酒后驾驶;血液浓度不低于80,属于醉酒驾驶。”2017年“中秋节”晚9点开始,济南市交警队在杆石桥交通岗前设点,对过往的车辆进行检查,经过4个小时,共查处喝过酒的驾驶者60名,下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。
,属于酒后驾驶;血液浓度不低于80,属于醉酒驾驶。”2017年“中秋节”晚9点开始,济南市交警队在杆石桥交通岗前设点,对过往的车辆进行检查,经过4个小时,共查处喝过酒的驾驶者60名,下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。
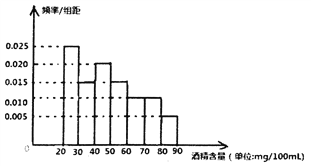
(1)求这60名驾驶者中属于醉酒驾车的人数(图中每组包括左端点,不包括右端点)
(2)若以各小组的中值为该组的估计值,频率为概率的估计值,求这60名驾驶者血液的酒精浓度的平均值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 各项均为正数,
各项均为正数, ![]() ,
, ![]() ,且
,且![]() 对任意
对任意![]() 恒成立,记
恒成立,记![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)证明:对任意正实数![]() ,
, ![]() 成等比数列;
成等比数列;
(3)是否存在正实数![]() ,使得数列
,使得数列![]() 为等比数列.若存在,求出此时
为等比数列.若存在,求出此时![]() 和
和![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,当直线
,当直线![]() 的倾斜角是
的倾斜角是![]() 时,
时, ![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() .
.

(1)求![]() 的值;
的值;
(2)以![]() 为直径的圆交
为直径的圆交![]() 轴于点
轴于点![]() ,记劣弧
,记劣弧![]() 的长度为
的长度为![]() ,当直线
,当直线![]() 绕
绕![]() 点旋转时,求
点旋转时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 是曲线
是曲线![]() 与直线
与直线![]() :
: ![]() (
(![]() )的交点(异于原点
)的交点(异于原点![]() ).
).
(1)写出![]() ,
, ![]() 的直角坐标方程;
的直角坐标方程;
(2)求过点![]() 和直线
和直线![]() 垂直的直线
垂直的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() -
-![]() ,g(x)=
,g(x)= ![]() .
.
(1)若![]() ,函数
,函数![]() 的图像与函数
的图像与函数![]() 的图像相切,求
的图像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 满足对任意
满足对任意![]() (x1
(x1![]() x2),都有
x2),都有![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,函数
,函数![]() =f(x)+ g(x),且G(
=f(x)+ g(x),且G(![]() )有两个极值点x1,x2,其中x1
)有两个极值点x1,x2,其中x1![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com