
【题目】已知数列![]() 各项均为正数,
各项均为正数, ![]() ,
, ![]() ,且
,且![]() 对任意
对任意![]() 恒成立,记
恒成立,记![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)证明:对任意正实数![]() ,
, ![]() 成等比数列;
成等比数列;
(3)是否存在正实数![]() ,使得数列
,使得数列![]() 为等比数列.若存在,求出此时
为等比数列.若存在,求出此时![]() 和
和![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
【答案】(1)![]() (2)见解析(3)存在
(2)见解析(3)存在![]() 使数列
使数列![]() 为等比数列,此时
为等比数列,此时![]() ,
, ![]() .
.
【解析】试题分析:(1)根据![]() ,
, ![]() ,且
,且![]() 对任意
对任意![]() 恒成立,代值计算即可.
恒成立,代值计算即可.
(2)a1=1,a2=2,且anan+3=an+1an+2对任意n∈N*恒成立,则可得![]() ,从而
,从而![]() 的奇数项和偶数项均构成等比数列,即可证明,
的奇数项和偶数项均构成等比数列,即可证明,
(3)在(2)中令![]() ,则数列
,则数列![]() 是首项为3,公比为
是首项为3,公比为![]() 的等比数列,从而得到
的等比数列,从而得到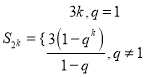 ,
, 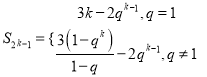 .又数列
.又数列![]() 为等比数列,解得
为等比数列,解得![]() ,∴
,∴![]() ,
, ![]() ,∴求出此时
,∴求出此时![]() 和
和![]() 的表达式.
的表达式.
试题解析:
解:(1)∵![]() ,∴
,∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ;
;
(2)由![]() ,两式相乘得
,两式相乘得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
从而![]() 的奇数项和偶数项均构成等比数列,
的奇数项和偶数项均构成等比数列,
设公比分别为![]() ,则
,则![]() ,
, ![]() ,
,
又∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,且
,且![]() 恒成立,
恒成立,
数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,问题得证;
的等比数列,问题得证;
(3)在(2)中令![]() ,则数列
,则数列![]() 是首项为3,公比为
是首项为3,公比为![]() 的等比数列,
的等比数列,
∴![]()
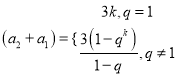
 ,
,
且![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∵数列![]() 为等比数列,∴
为等比数列,∴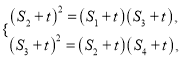
即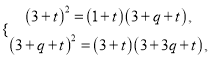 即
即![]()
解得![]() (
(![]() 舍去),
舍去),
∴![]() ,
, ![]() ,
,
从而对任意![]() 有
有![]() ,
,
此时![]() ,
, ![]() 为常数,满足
为常数,满足![]() 成等比数列,
成等比数列,
当![]() 时,
时, ![]() ,又
,又![]() ,∴
,∴![]() ,
,
综上,存在![]() 使数列
使数列![]() 为等比数列,此时
为等比数列,此时![]() ,
, ![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,分别求函数
时,分别求函数![]() 的最小值和
的最小值和![]() 的最大值,并证明当
的最大值,并证明当![]() 时,
时, ![]() 成立;
成立;
(3)令![]() ,当
,当![]() 时,判断函数
时,判断函数![]() 有几个不同的零点并证明.
有几个不同的零点并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程选讲.
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为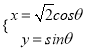 .
.
(1)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点M平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,若
两点,若![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
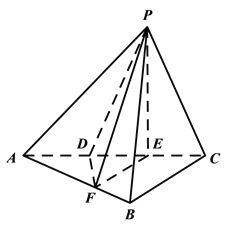
【题目】如图,三棱锥P-ABC中,平面PAC![]() 平面ABC,
平面ABC, ![]() ABC=
ABC=![]() ,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
,点D、E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF//BC.
(Ⅰ)证明:AB![]() 平面PFE.
平面PFE.
(Ⅱ)若四棱锥P-DFBC的体积为7,求线段BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
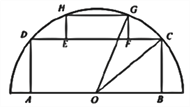
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池![]() 及其矩形附属设施
及其矩形附属设施![]() ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为
,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为![]() ,半径为
,半径为![]() ,矩形的一边
,矩形的一边![]() 在直径上,点
在直径上,点![]() 在圆周上,
在圆周上, ![]() 在边
在边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com