
(本题满分10分)
在极坐标系中,已知两点O(0,0),B(2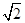 ,
,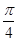 ).
).
(Ⅰ)求以OB为直径的圆C的极坐标方程,然后化成直角坐标方程;
(Ⅱ)以极点O为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,直线l的参数方程为
轴的正半轴建立平面直角坐标系,直线l的参数方程为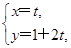 (t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(t为参数).若直线l与圆C相交于M,N两点,圆C的圆心为C,求DMNC的面积.
(1) (x-1)2+(y-1)2="2" (2)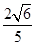
解析试题分析:解: (Ⅰ)设P(r,q)为圆上任意一点,则|OP|=r,ÐPOx=q-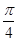 ,
,
在RtDPOB中,cos(q-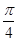 )=
)=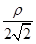 ,即r=2
,即r=2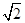 cos(q-
cos(q-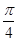 ).
).
∴r2=2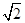 rcosq×
rcosq×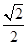 +2
+2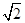 rsinq×
rsinq×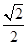 ,
,
∴圆C的直角坐标方程为(x-1)2+(y-1)2=2. ……5分
(Ⅱ)作CD^MN于D,C到直线l的距离为d= ,
,
在RtDCDA中,|MN|=2 =
= ,
,
∴S= ×
× ×
× =
=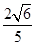 . ……10分
. ……10分
考点:本试题主要是对于坐标系与参数方程的考查。
点评:熟练掌握极坐标与直角坐标的互化,同时能利用直线与圆的位置关系,利用圆的半径,点到直线的距离公式以及弦长的关系来求解,并结合三角形正弦面积公式得到,属于中档题。


科目:高中数学 来源: 题型:解答题
如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D。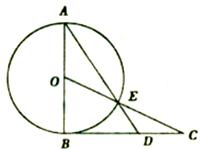
(1)求证:CE2 = CD · CB;
(2)若AB = BC = 2,求CE和CD的长。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知圆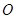 :
: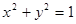 和定点
和定点 ,由圆外一点
,由圆外一点 向圆
向圆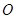 引切线
引切线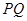 ,切点为
,切点为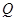 ,且满足
,且满足 .
.
(1)求实数 间满足的等量关系式;
间满足的等量关系式;
(2)求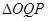 面积的最小值;
面积的最小值;
(3)求 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)
如图,AB是⊙O的直径 ,AC是弦 ,∠BAC的平分线AD交⊙O于点D,DE⊥AC,交AC的延长线于点E.OE交AD于点F.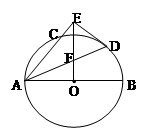
(1)求证:DE是⊙O的切线;
(2)若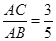 ,求
,求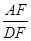 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4-1几何证明选讲
如图,AB是 O的直径,BE为圆0的切线,点c为
O的直径,BE为圆0的切线,点c为 o 上不同于A、B的一点,AD为
o 上不同于A、B的一点,AD为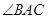 的平分线,且分别与BC 交于H,与
的平分线,且分别与BC 交于H,与 O交于D,与BE交于E,连结BD、CD.
O交于D,与BE交于E,连结BD、CD.
(I )求证:BD平分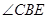
(II)求证:AH•BH=AE•HC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com