
【题目】![]() 个人在某个节日期间互通电话问候,已知其中每个人至多打通了三个朋友家的电话,任何两个人之间至多进行一次通话,且任何三个人中至少有两人,其中一个人打通了另一个人家里的电话,求
个人在某个节日期间互通电话问候,已知其中每个人至多打通了三个朋友家的电话,任何两个人之间至多进行一次通话,且任何三个人中至少有两人,其中一个人打通了另一个人家里的电话,求![]() 的最大值.
的最大值.
【答案】![]()
【解析】
先证明引理.
引理 ![]() 阶简单图
阶简单图![]() 中不存在
中不存在![]() ,则
,则![]() .
.
其中,![]() 表示
表示![]() 的边数.
的边数.
引理的证明:设![]() 是各项顶点中度最大的顶点,设与
是各项顶点中度最大的顶点,设与![]() 相邻的点的集合为
相邻的点的集合为![]() ,
,
与![]() 不相邻的点的集合为
不相邻的点的集合为![]()
![]() ,由于
,由于![]() 中无三角形,从而,
中无三角形,从而,![]() 在
在![]() 中没有边,则
中没有边,则![]() 的其他边都在
的其他边都在![]() 中或
中或![]() 之间,这样的边都是由顶点
之间,这样的边都是由顶点![]() 引出的.
引出的.
于是,![]()
![]() ,
,
又![]() ,所以,
,所以,![]() .
.
下面证明原题.
用![]() 个点表示
个点表示![]() 个人,如果一个人
个人,如果一个人![]() 打通了另一个人
打通了另一个人![]() 家里的电话,则连一条从
家里的电话,则连一条从![]() 到
到![]() 的有向边,得到一个简单的有向图
的有向边,得到一个简单的有向图![]() .
.
一方面,![]() 中无三角形,由引理有
中无三角形,由引理有![]() ,
,
故![]() ,
,
另一方面,![]() .
.
所以, ![]() , ①
, ①
当![]() 为奇数时,式①变为
为奇数时,式①变为![]() ,解得
,解得![]() ;
;
当![]() 为偶数时,式①变为
为偶数时,式①变为![]() ,解得
,解得![]() .
.
综上所述,![]() .
.
最后,![]() 是可能的,构造两个
是可能的,构造两个![]() ,对其中每个七边形
,对其中每个七边形![]() ,令
,令![]() 指向
指向![]() ,则构图合乎条件,
,则构图合乎条件,
首先,每个点作为始点都恰引出3条有向边,从而,每个人至多打通了3个朋友家的电话.
其次,对任何三个点,由抽屉原理知,必有两个点,![]() 在同一个
在同一个![]() 中,若
中,若![]() ,则
,则![]() 打通了
打通了![]() 家中的电话,若
家中的电话,若![]() 则
则![]() 打通了
打通了![]() 家中的电话.
家中的电话.


科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求:
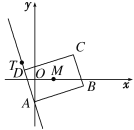
(1) AD边所在直线的方程;
(2) DC边所在直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地有A,B、C、D四人先后感染了新型冠状病毒,其中只有A到过疫区,B肯定是受A感染的,对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是![]() ,同样也假设D受A、B和C感染的概率都是
,同样也假设D受A、B和C感染的概率都是![]() .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量,写出X的可能取值为______,并求X的均值(即数学期望)为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在坐标原点,其焦点
的顶点在坐标原点,其焦点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 为直线
为直线![]() 上一点,圆
上一点,圆![]() 与
与![]() 轴相切(
轴相切(![]() 为圆心),且
为圆心),且![]() ,
,![]() 关于点
关于点![]() 对称.
对称.
(1)求圆![]() 和抛物线
和抛物线![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,交抛物线
两点,交抛物线![]() 于
于![]() ,
,![]() 两点,求证:
两点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆周上依次有![]() 个点
个点![]() ,今随机地选取其中
,今随机地选取其中![]() 个点为顶点作凸
个点为顶点作凸![]() 边形
边形![]() ,已知选取与否的可能性是相同的,试求对每个
,已知选取与否的可能性是相同的,试求对每个![]() ,
,![]() 边形的两个相邻顶点
边形的两个相邻顶点![]() (规定
(规定![]() )之间至少有
)之间至少有![]() 中的
中的![]() 个点的概率,其中,
个点的概率,其中,![]() 是给定的一组正整数.
是给定的一组正整数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有A、B、C三人进行乒乓球比赛,当其中两个人比赛时,另一个人作裁判,此场比赛的输者在下一场中当裁判,另两个人接着比赛.比赛进行了若干场以后,已知A共赛了a场,B共赛了b场.求C赛的场数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:![]() )有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间
)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时,
(单位:瓶)为多少时,![]() 的数学期望达到最大值?
的数学期望达到最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一袋中有标有号码1、2、3、4的卡片各一张,每次从中取出一张,记下号码后放回,当四种号码的卡片全部取出时即停止,则恰好取6次卡片时停止的概率为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com