Question

（08年朝阳区综合练习一）（13分）

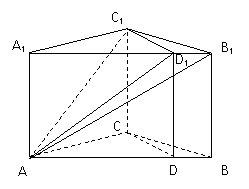
直三棱柱ABC-A₁B₁C₁中，∠ACB=120°，AC=CB=A₁A=1，D₁是A₁B₁上一动点(可

以与A₁或B₁重合），过D₁和C₁C的平面与AB交于D.

（Ⅰ）证明BC∥平面AB₁C₁；

（Ⅱ）若D₁为A₁B₁的中点，求三棱

锥B₁-C₁AD₁的体积；

（Ⅲ）求二面角D₁-AC₁-C的取值范围.

 

Answer 1

解析：方法1：

（Ⅰ）证明：依条件有CB∥C₁B₁，

 又C₁B₁平面A B₁C₁，

CB平面A B₁C₁，

所以CB∥平面A B₁C₁.…………………3分

 

（Ⅱ）解：

     因为D为AB的中点，

     依条件可知C₁D⊥A₁B₁.

所以=

=×C₁D₁×(×A₁A×D₁B₁)

= ××(×1×)=.………………………………………………………7分

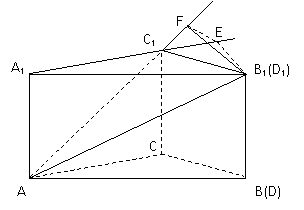
（Ⅲ）解：

因为D₁是A₁B₁上一动点，

 所以当D₁与A₁重合时，二面角D₁-

AC₁-C的大小为π；    ……………………………………………………………9分

当D₁与B₁重合时，

如图，分别延长A₁C₁和AC₁，

过B₁作B₁E⊥A₁C₁延长于E，

依条件可知平面A₁B₁C₁⊥平面

ACC₁A₁，

所以B₁E⊥平面ACC₁A₁.

     过点E作EF⊥A₁C₁，垂直为F.

     连结FB₁，

     所以FB₁⊥A₁C₁.

     所以∠B₁FE是所求二面角的平面角.   ……………………………………………11分

     容易求出B₁E=，FE=.

     所以tan∠B₁FE==.

所以∠B₁FE= arctan. （或arccos）

所以二面角D₁-AC₁-C的取值范围是[arctan，π]（或[arccos，π]）.……13分

 

方法2：

 

（Ⅰ），（Ⅱ）略

（Ⅲ）解：

如图建立空间直角坐标系，

 

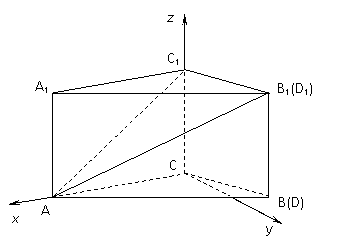
则有A(1，0，0)，B₁(-，，1)，

C₁(0，0，1).

 因为D₁是A₁B₁上一动点，

 所以当D₁与A₁重合时，二面角

D₁-AC₁-C的大小为π；……………………………………………………………9分

当D₁与B₁重合时，

 显然向量n₁=(0，1，0)是平面A

CC₁A₁的一个法向量.

     因为=(1，0，-1)，

     =(-，，1)，

设平面C₁AB₁的法向量是n₂=(x，y，z)，

由?n₂=0，?n₂=0，解得平面C₁AB₁的一个法向量n₂=(1，，1).

因为n₁?n₂=，| n₁|=1，| n₂|=，

设二面角B₁-AC₁-C的大小为β，

所以cosβ=.

即β=arccos.

所以二面角D₁-AC₁-C的取值范围是[arccos，π]（或[arctan，π]）.…13分