
【题目】甲袋中装有2个白球,3个黑球,乙袋中装有1个白球,2个黑球,这些球除颜色外完全相同.
(1)从两袋中各取1个球,记事件![]() :取出的2个球均为白球,求
:取出的2个球均为白球,求![]() ;
;
(2)每次从甲、乙两袋中各取2个球,若取出的白球不少于2个就获奖(每次取完后将球放回原袋),共取了3次,记获奖次数为![]() ,写出
,写出![]() 的分布列并求
的分布列并求![]() .
.
【答案】(1)![]() (2)见解析,
(2)见解析,![]()
【解析】
(1)根据甲袋中装有2个白球,3个黑球,乙袋中装有1个白球,2个黑球,先求出从两袋中各取1个球基本事件的总数,再求出取出的2个球均为白球的事件数,利用古典概型公式求解.
(2)先求出一次中获奖的概率:再确定在3次游戏中获奖的次数的所有可能取值为0,1,2,3,求出相应的概率,即可写出分布列.
(1)根据题意,甲袋中装有2个白球,3个黑球,从中取1球有![]() 种,乙袋中装有1个白球,2个黑球,从中取1球有
种,乙袋中装有1个白球,2个黑球,从中取1球有![]() 种,从两袋中各取1个球共有
种,从两袋中各取1个球共有![]() 种,取出的2个球均为白球共有
种,取出的2个球均为白球共有![]() 种,
种,
所以![]() .
.
(2)![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,
一次中获奖的概率:![]() ,
,
一次中不获奖的概率:![]() ,
,
所以![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列为:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】在疫情防控过程中,某医院一次性收治患者127人.在医护人员的精心治疗下,第15天开始有患者治愈出院,并且恰有其中的1名患者治愈出院.如果从第16天开始,每天出院的人数是前一天出院人数的2倍,那么第19天治愈出院患者的人数为_______________,第_______________天该医院本次收治的所有患者能全部治愈出院.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() :
:![]() (
(![]() 为参数),
为参数),![]() 与
与![]() 相切于点
相切于点![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求![]() 的极坐标方程及点
的极坐标方程及点![]() 的极坐标;
的极坐标;
(2)已知直线![]() :
:![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,记
两点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点
的左、右焦点![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,且
上的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)若![]() 是椭圆
是椭圆![]() 的左、右顶点,直线
的左、右顶点,直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)某县一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨、硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨、硝酸盐15吨.先库存磷酸盐10吨、硝酸盐66吨,在此基础上生产这两种混合肥料.若生产1车皮甲种肥料产生的利润为10000元;生产1车皮乙种肥料产生的利润为5000元.那么分别生产甲、乙两种肥料各多少车皮能产生最大的利润?
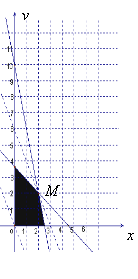
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】车工刘师傅利用数控车床为某公司加工一种高科技易损零件,对之前加工的100个零件的加工时间进行统计,结果如下:
加工1个零件用时 | 20 | 25 | 30 | 35 |
频数(个) | 15 | 30 | 40 | 15 |
以加工这100个零件用时的频率代替概率.
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘师傅准备给几个徒弟做一个加工该零件的讲座,用时40分钟,另外他打算在讲座前、讲座后各加工1个该零件作示范.求刘师傅讲座及加工2个零件作示范的总时间不超过100分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入![]() ,
,![]() 的值分别为5,2,则输出
的值分别为5,2,则输出![]() 的值为( )
的值为( )
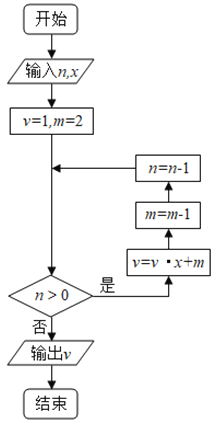
A.64B.68C.72D.133
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com