【题目】已知函数
，
.
（1）求
的单调区间及最小值；
（2）若在区间
上不等式
恒成立，求实数
的取值范围.
【答案】（1）
的增区间为
，减区间为
，最小值为
；（2）
.
【解析】
试题分析：（1）对函数进行求导，令
，
对应的不等式的解即为相对应的单调区间，结合单调性求最值；（2）不等式
恒成立等价于s恒成立，求
，利用其求
得最小值，在其中将要用到二次求导及分类讨论.
试题解析：（1）由
，
当
时，
，是减函数，
当
时，
，是增函数，
的最小值为
，
所以的增区间为，减区间为，最小值为
.
（2）设函数
，
，
则
因为，所以
的符号就是
的符号.
设
，，则
，
因为，所以
，
①当
时，
，
在
上是增函数，又
，所以
， 
，
在上是增函数，又
，所以
，
故合乎题意
②当
时，由
得
，在区间
上，
，是减函数，所 以 在区间
内，
，所以
，在上是减函数，
，故不合题意综上所述，所求的实数
的取值范围为
科目：高中数学 来源： 题型：
【题目】对于定义域为
的函数
，如果存在区间
，同时满足：
①
在
上是单调函数；
②当定义域是
时，
的值域也是
．
则称
是该函数的“等域区间”．
（1）求证：函数
不存在“等域区间”；
（2）已知函数
（
，
）有“等域区间”
，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某商店计划每天购进某商品若干件，商店每销售一件该商品可获利润60元，若供大于求，剩余商品全部退回，但每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利40元.
（1）若商品一天购进该商品10件，求当天的利润
（单位：元）关于当天需求量
（单位：件，
）的函数解析式；
（2）商店记录了50天该商品的日需求量
（单位：件，
），整理得下表：
若商店一天购进10件该商品，以50天记录的各需求量的频率作为各需求量发生的概率，求当天的利润在区间
内的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在如下图象中的两条线段上．该股票在30天内（包括30天）的日交易量Q（万股）与时间t（天）的部分数据如下表所示：
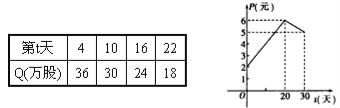
（1）根据提供的图象，写出该种股票每股的交易价格P（元）与时间t（天）所满足的函数关系式；
（2）根据表中数据确定日交易量Q（万股）与时间t（天）的一次函数关系式；
（3）用y（万元）表示该股票日交易额，写出y关于t的函数关系式，并求出这30天中第几天日交易额最大，最大值为多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
