
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() Ķń÷ĪĹ«ĪŖOA‘ŕx÷Š…Ō£¨∂•Ķ„BĶń◊ÝĪÍő™
Ķń÷ĪĹ«ĪŖOA‘ŕx÷Š…Ō£¨∂•Ķ„BĶń◊ÝĪÍő™![]() £¨÷ĪŌŖCDĹĽAB”ŕĶ„
£¨÷ĪŌŖCDĹĽAB”ŕĶ„![]() £¨ĹĽx÷Š”ŕĶ„
£¨ĹĽx÷Š”ŕĶ„![]() .
.

(1)«ů÷ĪŌŖCDĶń∑Ĺ≥Ő£Ľ
(2)∂ĮĶ„P‘ŕx÷Š…Ōī”Ķ„![]() ≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»ŌÚx÷Š’ż∑ĹŌÚ‘ň∂Į£¨ĻżĶ„P◊ų÷ĪŌŖlīĻ÷Ī”ŕx÷Š£¨…Ť‘ň∂Į Īľšő™t.
≥Ų∑Ę£¨“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»ŌÚx÷Š’ż∑ĹŌÚ‘ň∂Į£¨ĻżĶ„P◊ų÷ĪŌŖlīĻ÷Ī”ŕx÷Š£¨…Ť‘ň∂Į Īľšő™t.
ĘŔĶ„P‘ŕ‘ň∂ĮĻż≥Ő÷–£¨ «∑Ůīś‘ŕń≥łŲőĽ÷√£¨ ĻĶ√![]() ?»Űīś‘ŕ£¨«Ž«ů≥ŲĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
?»Űīś‘ŕ£¨«Ž«ů≥ŲĶ„PĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£Ľ
Ęŕ«ŽŐĹňųĶĪtő™ļő÷Ķ Ī£¨‘ŕ÷ĪŌŖl…Ōīś‘ŕĶ„M£¨‘ŕ÷ĪŌŖCD…Ōīś‘ŕĶ„Q£¨ ĻĶ√“‘OBő™“ĽĪŖ£¨O£¨B£¨M£¨Qő™∂•Ķ„ĶńňńĪŖ–őő™Ń‚–ő£¨≤Ę«ů≥Ųīň ĪtĶń÷Ķ.
°ĺīūįł°Ņ(1)![]() £Ľ(2)ĘŔ¬ķ◊„ŐűľĢĶńĶ„P◊ÝĪÍő™
£Ľ(2)ĘŔ¬ķ◊„ŐűľĢĶńĶ„P◊ÝĪÍő™![]() ĽÚ
ĽÚ![]() £¨Ęŕ¬ķ◊„ŐűľĢĶńtĶń÷Ķő™
£¨Ęŕ¬ķ◊„ŐűľĢĶńtĶń÷Ķő™![]() ĽÚ
ĽÚ![]() .
.
°ĺĹ‚őŲ°Ņ
£®1£©ņŻ”√ŃĹĶ„ Ĺ«ů≥Ų÷ĪŌŖ∑Ĺ≥Ő£¨‘ŔĽĮő™“Ľį„∑Ĺ≥Ő£Ľ
£®2£©ĘŔłýĺ›Ő‚“‚◊ųDP°őOB£¨ņŻ”√Ōŗň∆»żĹ«–ő«ů≥ŲĶ„PĶń◊ÝĪÍ£¨łýĺ›∂‘≥∆–‘«ůĶ√P°šĶń◊ÝĪÍ£Ľ
Ęŕ∑÷«ťŅŲŐ÷¬Ř£¨OP£ĹOB£Ĺ10 Ī£¨◊ųPQ°őOBĹĽCD”ŕQ£¨«ůĶ√Ķ„M”ŽĶ„P÷ōļŌ£¨t£Ĺ0£Ľ
OQ£ĹOB Ī£¨«ů≥ŲĶ„QĶńļŠ◊ÝĪÍ£¨ľ∆ň„MĶńļŠ◊ÝĪÍ£¨«ůĶ√tĶń÷Ķ£ĽQĶ„”ŽCĶ„÷ōļŌ Ī£¨«ůĶ√MĶ„ĶńļŠ◊ÝĪÍ£¨Ķ√≥ŲtĶń÷Ķ.
Ĺ‚£ļ£®1£©÷ĪŌŖCDĻżĶ„C£®12£¨0£©£¨D£®6£¨3£©£¨
÷ĪŌŖ∑Ĺ≥Őő™![]() £Ĺ
£Ĺ![]() £¨
£¨
ĽĮő™“Ľį„–ő Ĺ «x+2y©Ā12£Ĺ0£Ľ
£®2£©ĘŔ»ÁÕľ1÷–£¨
◊ųDP°őOB£¨‘Ú°ŌPDA£Ĺ°ŌB£¨
”…DP°őOBĶ√£¨![]() £Ĺ
£Ĺ![]() £¨ľī
£¨ľī![]() £Ĺ
£Ĺ![]() £¨°ŗPA£Ĺ
£¨°ŗPA£Ĺ![]() £Ľ
£Ľ
°ŗOP£Ĺ6©Ā![]() £Ĺ
£Ĺ![]() £¨°ŗĶ„P£®
£¨°ŗĶ„P£®![]() £¨0£©£Ľ
£¨0£©£Ľ
łýĺ›∂‘≥∆–‘÷™£¨ĶĪAP£ĹAP°š Ī£¨P°š£®![]() £¨0£©£¨
£¨0£©£¨
°ŗ¬ķ◊„ŐűľĢĶńĶ„P◊ÝĪÍő™£®![]() £¨0£©ĽÚ£®
£¨0£©ĽÚ£®![]() £¨0£©£Ľ
£¨0£©£Ľ
Ęŕ»ÁÕľ2÷–£¨ĶĪOP£ĹOB£Ĺ10 Ī£¨◊ųPQ°őOBĹĽCD”ŕQ£¨
‘Ú÷ĪŌŖOBĶńĹ‚őŲ Ĺő™y£Ĺ![]() x£¨
x£¨
÷ĪŌŖPQĶńĹ‚őŲ Ĺő™y£Ĺ![]() x+
x+![]() £¨
£¨
”… £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £¨°ŗQ£®©Ā4£¨8£©£Ľ
£¨°ŗQ£®©Ā4£¨8£©£Ľ
°ŗPQ£Ĺ![]() £Ĺ10£¨
£Ĺ10£¨
°ŗPQ£ĹOB£¨°ŗňńĪŖ–őOPQB «∆Ĺ––ňńĪŖ–ő£¨
”÷OP£ĹOB£¨°ŗ∆Ĺ––ňńĪŖ–őOPQB «Ń‚–ő£Ľ
īň ĪĶ„M”ŽĶ„P÷ōļŌ£¨«“t£Ĺ0£Ľ
»ÁÕľ3£¨ĶĪOQ£ĹOB Ī£¨…ŤQ£®m£¨©Ā![]() m+6£©£¨
m+6£©£¨
‘Ú”–m2+ £Ĺ102£¨
£Ĺ102£¨
Ĺ‚Ķ√m£Ĺ![]() £Ľ
£Ľ
°ŗĶ„QĶńļŠ◊ÝĪÍő™![]() ĽÚ
ĽÚ![]() £Ľ
£Ľ
…ŤMĶńļŠ◊ÝĪÍő™a£¨
‘Ú![]() £Ĺ
£Ĺ ĽÚ
ĽÚ![]() £Ĺ
£Ĺ £¨
£¨
Ĺ‚Ķ√a£Ĺ![]() ĽÚa£Ĺ
ĽÚa£Ĺ![]() £Ľ
£Ľ
”÷Ķ„P «ī”Ķ„£®©Ā10£¨0£©Ņ™ ľ‘ň∂Į£¨
‘Ú¬ķ◊„ŐűľĢĶńtĶń÷Ķő™![]() ĽÚ
ĽÚ![]() £Ľ
£Ľ
»ÁÕľ4£¨ĶĪQĶ„”ŽCĶ„÷ōļŌ Ī£¨MĶ„ĶńļŠ◊ÝĪÍő™6£¨īň Īt£Ĺ16£Ľ
◊Ř…Ō£¨¬ķ◊„ŐűľĢĶńt÷Ķő™0£¨ĽÚ16£¨ĽÚ![]() ĽÚ
ĽÚ![]() .
.






 Īł’Ĺ÷–ŅľļģľŔŌĶŃ–īūįł
Īł’Ĺ÷–ŅľļģľŔŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
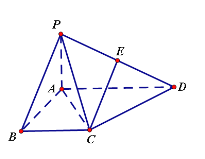
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨ňńņ‚◊∂![]() ÷–£¨
÷–£¨![]() Ķ◊√ś
Ķ◊√ś![]() £¨
£¨![]() £¨Ķ◊√ś
£¨Ķ◊√ś![]() «÷ĪĹ«Ő›–ő£¨
«÷ĪĹ«Ő›–ő£¨![]() .
.
£®ĘŮ£©«ů÷§£ļ∆Ĺ√ś![]() ∆Ĺ√ś
∆Ĺ√ś![]() £Ľ
£Ľ
£®ĘÚ£©‘ŕņ‚![]() …Ō «∑Ůīś‘ŕ“ĽĶ„
…Ō «∑Ůīś‘ŕ“ĽĶ„![]() £¨ Ļ
£¨ Ļ![]() //∆Ĺ√ś
//∆Ĺ√ś![]() £Ņ»Űīś‘ŕ£¨«Ž»∑∂®
£Ņ»Űīś‘ŕ£¨«Ž»∑∂®![]() Ķ„ĶńőĽ÷√£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
Ķ„ĶńőĽ÷√£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”….
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™’żŌÓ żŃ–![]() Ķń«įnŌÓļÕ
Ķń«įnŌÓļÕ![]() ¬ķ◊„
¬ķ◊„![]()
£®1£©«ů żŃ–![]() ĶńÕ®ŌÓĻę Ĺ£Ľ
ĶńÕ®ŌÓĻę Ĺ£Ľ
£®2£©»Ű £®n° N*£©£¨«ů żŃ–
£®n° N*£©£¨«ů żŃ–![]() Ķń«įnŌÓļÕ
Ķń«įnŌÓļÕ![]() ;
;
£®3£© «∑Ůīś‘ŕ Ķ ż![]() ĻĶ√
ĻĶ√![]() ∂‘
∂‘![]() ļ„≥…ŃĘ£¨»Űīś‘ŕ£¨«ů Ķ ż
ļ„≥…ŃĘ£¨»Űīś‘ŕ£¨«ů Ķ ż![]() Ķń»°÷Ķ∑∂őߣ¨»Ű≤Ľīś‘ŕňĶ√ųņŪ”…£ģ
Ķń»°÷Ķ∑∂őߣ¨»Ű≤Ľīś‘ŕňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥≥Ķľš◊‚Ńřľ◊°Ę““ŃĹ÷÷…ŤĪł…ķ≤ķA£¨BŃĹņŗ≤ķ∆∑£¨ľ◊÷÷…ŤĪł√ŅŐžń‹…ķ≤ķAņŗ≤ķ∆∑8ľĢļÕBņŗ≤ķ∆∑15ľĢ£¨““÷÷…ŤĪł√ŅŐžń‹…ķ≤ķAņŗ≤ķ∆∑10ľĢļÕBņŗ≤ķ∆∑25ľĢ£¨“—÷™…ŤĪłľ◊√ŅŐžĶń◊‚Ńř∑—300‘™£¨…ŤĪł““√ŅŐžĶń◊‚Ńř∑—400‘™£¨Ō÷≥Ķľš÷Ń…Ŕ“™…ķ≤ķAņŗ≤ķ∆∑100ľĢ£¨Bņŗ≤ķ∆∑200ľĢ£¨ňý–Ť◊‚Ńř∑—◊Ó…Ŕő™__‘™![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ…ŤÕ÷‘≤![]() Ķń◊ů°Ę”“ĹĻĶ„∑÷Īūő™
Ķń◊ů°Ę”“ĹĻĶ„∑÷Īūő™![]() °Ę
°Ę![]() £¨Ļż
£¨Ļż![]() Ķń÷ĪŌŖĹĽÕ÷‘≤”ŕ
Ķń÷ĪŌŖĹĽÕ÷‘≤”ŕ![]() £¨
£¨![]() ŃĹĶ„£¨»ŰÕ÷‘≤
ŃĹĶ„£¨»ŰÕ÷‘≤![]() ĶńņŽ–ń¬ ő™
ĶńņŽ–ń¬ ő™![]() £¨
£¨![]() Ķń÷‹≥§ő™16£ģ
Ķń÷‹≥§ő™16£ģ
£®1£©«ůÕ÷‘≤![]() Ķń∑Ĺ≥Ő£Ľ
Ķń∑Ĺ≥Ő£Ľ
£®2£©…Ť≤Ľĺ≠ĻżÕ÷‘≤Ķń÷––ń∂Ý∆Ĺ––”ŕŌ“![]() Ķń÷ĪŌŖĹĽÕ÷‘≤
Ķń÷ĪŌŖĹĽÕ÷‘≤![]() ”ŕĶ„
”ŕĶ„![]() £¨
£¨![]() £¨…ŤŌ“
£¨…ŤŌ“![]() £¨
£¨![]() Ķń÷–Ķ„∑÷Īūő™
Ķń÷–Ķ„∑÷Īūő™![]() £¨
£¨![]() £ģ÷§√ų£ļ
£ģ÷§√ų£ļ![]() £¨
£¨![]() £¨
£¨![]() »żĶ„Ļ≤ŌŖ£ģ
»żĶ„Ļ≤ŌŖ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘໿ņ‚◊∂![]() ÷–£¨
÷–£¨![]() ∆Ĺ√ś
∆Ĺ√ś![]() £¨“—÷™
£¨“—÷™![]() £¨Ķ„
£¨Ķ„![]() ∑÷Īūő™
∑÷Īūő™![]() Ķń÷–Ķ„.
Ķń÷–Ķ„.

£®1£©«ů÷§£ļ![]() £Ľ
£Ľ
£®2£©»ŰF‘ŕŌŖ∂ő![]() …Ō£¨¬ķ◊„
…Ō£¨¬ķ◊„![]() ∆Ĺ√ś
∆Ĺ√ś![]() £¨«ů
£¨«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®3£©»Ű»żĹ«–ő![]() «’ż»żĹ«–ő£¨ĪŖ≥§ő™2£¨«ů∂Ģ√śĹ«
«’ż»żĹ«–ő£¨ĪŖ≥§ő™2£¨«ů∂Ģ√śĹ«![]() Ķń’ż«–÷Ķ.
Ķń’ż«–÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ňę«ķŌŖC1£ļ![]() -
-![]() =1£ģ
=1£ģ
£®1£©»ŰĶ„M£®3£¨t£©‘ŕňę«ķŌŖC1…Ō£¨«ůMĶ„ĶĹňę«ķŌŖC1”“ĹĻĶ„ĶńĺŗņŽ£Ľ
£®2£©«ů”Žňę«ķŌŖC1”–Ļ≤Õ¨Ĺ•ĹŁŌŖ£¨«“ĻżĶ„£®-3£¨2![]() £©Ķńňę«ķŌŖC2ĶńĪÍ◊ľ∑Ĺ≥Ő£ģ
£©Ķńňę«ķŌŖC2ĶńĪÍ◊ľ∑Ĺ≥Ő£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļłŖ÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ“—÷™ļĮ ż![]()
£®![]() £©ĶĪ
£©ĶĪ![]() Ī£¨«ů
Ī£¨«ů![]() ĶńĶ•Ķų«ÝľšļÕľę÷Ķ.
ĶńĶ•Ķų«ÝľšļÕľę÷Ķ.
£®![]() £©»Ű∂‘”ŕ»ő“‚
£©»Ű∂‘”ŕ»ő“‚![]() £¨∂ľ”–
£¨∂ľ”–![]() ≥…ŃĘ£¨«ů
≥…ŃĘ£¨«ů![]() Ķń»°÷Ķ∑∂őß £Ľ
Ķń»°÷Ķ∑∂őß £Ľ
£®![]() £©»Ű
£©»Ű![]() «“
«“![]() ÷§√ų£ļ
÷§√ų£ļ![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com