
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() 时,
时,![]() .
.

(1)求函数![]() 的解析式,并画出函数图像;
的解析式,并画出函数图像;
(2)写出函数![]() 的单调区间及值域;
的单调区间及值域;
(3)求使![]() 恒成立的实数
恒成立的实数![]() 的取值范围.
的取值范围.
(注明:(2)(3)可直接写出答案,不要求写出解答过程)
【答案】(1)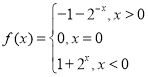 ;(2)
;(2)![]() 的单调递增区间为
的单调递增区间为![]() ,值域为
,值域为![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据奇函数的性质,结合函数在![]() 时的解析式,可得
时的解析式,可得![]() 在
在![]() 上的解析式;根据指数函数的图象以及平移的相关知识可先作出
上的解析式;根据指数函数的图象以及平移的相关知识可先作出![]() 时的图象,再根据奇函数的性质作出
时的图象,再根据奇函数的性质作出![]() 时的图象;(2)根据函数的图象可得函数的单调区间,值域;(3)根据函数的图象可得函数的最小值.
时的图象;(2)根据函数的图象可得函数的单调区间,值域;(3)根据函数的图象可得函数的最小值.
试题解析:(1)设![]() ,则
,则![]() ,
,![]() ,
,
![]()
![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
∴![]() ,且
,且![]() ,
,
![]() ,即
,即![]() ,
,
![]() 函数
函数![]() 的解析式为
的解析式为 ........4分
........4分
(2)由图可知,函数![]() 的单调递增区间为
的单调递增区间为![]() ;........... 8分
;........... 8分
值域为![]() ................10分
................10分
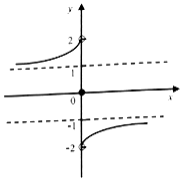
(3)由图可知,要使![]() 恒成立,实数
恒成立,实数![]() 的取值范围为
的取值范围为![]() .........12分
.........12分


科目:高中数学 来源: 题型:
【题目】甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本
(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本![]() 固定成本+生产成本),销售收入
固定成本+生产成本),销售收入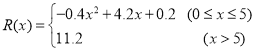 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入—总成本);
销售收入—总成本);
(2)甲厂生产多少台新产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政策,整个社会将会出现一系列的问题,若某地区2015年人口总数为![]() 万,实施“放开二胎”新政策后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加
万,实施“放开二胎”新政策后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加![]() 万人,从2026年开始到2035年每年人口为上一年的
万人,从2026年开始到2035年每年人口为上一年的![]() .
.
(1)求实施新政策后第![]() 年的人口总数
年的人口总数![]() 的表达式(注:2016年为第一年);
的表达式(注:2016年为第一年);
(2)若新政策实施后的2016年到2035年人口平均值超过![]() 万,则需调整政策,否则继续实施,问到2035年后是否需要调整政策?(说明:
万,则需调整政策,否则继续实施,问到2035年后是否需要调整政策?(说明:![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与![]() 轴非负半轴重合,直线
轴非负半轴重合,直线![]() 的参数方程为:
的参数方程为:
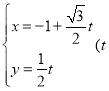 为参数),曲线
为参数),曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从遂宁市中、小学生中抽取部分学生,进行肺活量调查.经了解,我市小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是
A. 简单的随机抽样 B. 按性别分层抽样
C. 按学段分层抽样 D. 系统抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com