
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在![]() 岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间
岁之间的200人进行调查.并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”
内的人分别称为“青少年人”和“中老年人”![]() 经统计“青少年人”和“中老年人”的人数之比为
经统计“青少年人”和“中老年人”的人数之比为![]() ,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
,其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.
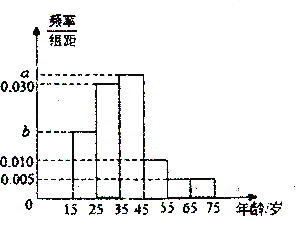
(1)求图中a,b的值;
(2)现采用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
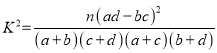
P(K2≥k0) | 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
k0 | 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 列联表见解析;有
列联表见解析;有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”.
的把握认为“中老年人”比“青少年人”更加关注“两会”.
【解析】
(1)根据“青少年人”和“中老年人”的人数之比,结合频率分布直方图可构造方程求得结果;
(2)由分层抽样原则可确定从![]() 中抽取
中抽取![]() 人,从
人,从![]() 中抽取
中抽取![]() 人,采用列举法得到所有基本事件和满足题意的基本事件个数,由古典概型概率公式求得结果;
人,采用列举法得到所有基本事件和满足题意的基本事件个数,由古典概型概率公式求得结果;
(3)利用频率和总数计算得到频数,由此完成![]() 列联表,计算可得
列联表,计算可得![]() ,由独立性检验的思想可得到结果.
,由独立性检验的思想可得到结果.
(1)![]() “青少年人”和“中老年人”的人数之比为
“青少年人”和“中老年人”的人数之比为![]() ,
,
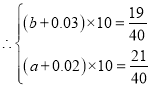 ,解得:
,解得:![]() .
.
(2)由分层抽样原则知:从![]() 中应抽取
中应抽取![]() 人,从
人,从![]() 中应抽取
中应抽取![]() 人;
人;
记从![]() 中抽取的
中抽取的![]() 人为:
人为:![]() ;从
;从![]() 中抽取的
中抽取的![]() 人为
人为![]() .
.
则从![]() 人中任取
人中任取![]() 人,有
人,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种情况;
种情况;
其中至少有![]() 人是“中老年人”的情况有:
人是“中老年人”的情况有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种情况,
种情况,
![]() 所求概率
所求概率![]() .
.
(3)“青少年人”共有![]() 人,“中老年人”共有
人,“中老年人”共有![]() 人,
人,
则可得![]() 列联表如下:
列联表如下:
关注 | 不关注 | 合计 | |
青少年人 |
|
|
|
中老年人 |
|
|
|
合计 |
|
|
|
![]() ,
,
![]() 有
有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”.
的把握认为“中老年人”比“青少年人”更加关注“两会”.


科目:高中数学 来源: 题型:
【题目】等差数列![]() 和等比数列
和等比数列![]() 中,
中, ![]() ,
,![]() ,
,![]() 是
是![]() 前
前![]() 项和.
项和.
(1)若 ![]() ,求实数
,求实数![]() 的值;
的值;
(2)是否存在正整数![]() ,使得数列
,使得数列![]() 的所有项都在数列
的所有项都在数列![]() 中?若存在,求出所有的
中?若存在,求出所有的![]() ,若不存在,说明理由;
,若不存在,说明理由;
(3)是否存在正实数![]() ,使得数列
,使得数列![]() 中至少有三项在数列
中至少有三项在数列![]() 中,但
中,但![]() 中的项不都在数列
中的项不都在数列![]() 中?若存在,求出一个可能的
中?若存在,求出一个可能的![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假如你的公司计划购买台机器,该种机器使用三年后即被淘汰,在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元,在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费,现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记![]() 表示1台机器在三年使用期内的维修次数,
表示1台机器在三年使用期内的维修次数,![]() 表示1台机器在维修上所需的费用(单位:元),
表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求
”的频率不小于0.8,求![]() 的值.
的值.
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
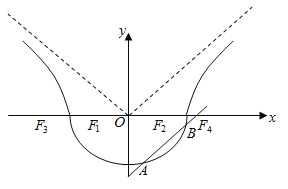
【题目】已知![]() ,如图,曲线
,如图,曲线![]() 由曲线
由曲线![]() :
:![]() 和曲线
和曲线![]() :
:![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点.
所在圆锥曲线的焦点.
(Ⅰ)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)如图,作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点
于点![]() ,求证:弦
,求证:弦![]() 的中点
的中点![]() 必在曲线
必在曲线![]() 的另一条渐近线上;
的另一条渐近线上;
(Ⅲ)对于(Ⅰ)中的曲线![]() ,若直线
,若直线![]() 过点
过点![]() 交曲线
交曲线![]() 于点
于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )的焦点
)的焦点![]() 到点
到点![]() 的距离为
的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在第一和第二象限内,求
分别在第一和第二象限内,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】健身馆某项目收费标准为每次60元,现推出会员优惠活动:具体收费标准如下:
消费次数 | 第1次 | 第2次 | 第3次 | 不少于4次 |
收费比例 | 0.95 | 0.90 | 0.85 | 0.80 |
现随机抽取了100位会员统计它们的消费次数,得到数据如下:
消费次数 | 1次 | 2次 | 3次 | 不少于4次 |
频数 | 60 | 25 | 10 | 5 |
假设该项目的成本为每次30元,根据给出的数据回答下列问题:
(1)估计1位会员至少消费两次的概率
(2)某会员消费4次,求这4次消费获得的平均利润;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1+a2+…+an=an+1﹣2.
(1)若a1=2,求数列{an}的通项公式;
(2)若数列1,a2,a4,b1,b2,…bn,…成等差数列,求数列{bn}的前n项和为Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国在贵州省平塘县境内修建的500米口径球面射电望远镜(FAST)是目前世界上最大单口径射电望远镜.使用三年来,已发现132颗优质的脉冲星候选体,其中有93颗已被确认为新发现的脉冲星,脉冲星是上世纪60年代天文学的四大发现之一,脉冲星就是正在快速自转的中子星,每一颗脉冲星每两脉冲间隔时间(脉冲星的自转周期)是-定的,最小小到0.0014秒,最长的也不过11.765735秒.某-天文研究机构观测并统计了93颗已被确认为新发现的脉冲星的自转周期,绘制了如图的频率分布直方图.

(1)在93颗新发现的脉冲星中,自转周期在2至10秒的大约有多少颗?
(2)根据频率分布直方图,求新发现脉冲星自转周期的平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com