
ĄūĖâÄŋĄŋÄģÐĢΊĖáļßŋÎĖÃ―ĖŅ§Ð§đûĢŽŨî―üÁĒÏîÁËĘОķŋÎĖâĄķļßЧŋÎĖÃ―ĖŅ§ÄĢĘ―ž°ÆäÔËÓÃĄ·ĢŽÆäÖÐÍõĀÏĘĶĘĮļÃŋÎĖâĩÄÖũŅÐČËÖŪŌŧĢŽÎŠŧņĩÃĩÚŌŧĘÖĘýūÝĢŽËý·ÖąðÔÚžŨĄĒŌŌÁ―ļöÆ―ÐаāēÉÓÃĄ°īŦÍģ―ĖŅ§ĄąšÍĄ°ļßЧŋÎĖÃĄąÁ―ÖÖēŧÍŽĩÄ―ĖŅ§ÄĢĘ――øÐÐ―ĖŅ§ĘĩŅé.ΊÁË―â―ĖļÄĘĩЧĢŽÆÚÖÐŋžĘÔšóĢŽ·ÖąðīÓÁ―ļö°āžķÖÐļũËæŧúģéČĄ20ÃûŅ§ÉúĩÄģÉžĻ―øÐÐÍģžÆĢŽŨũģöČįÍžËųĘūĩÄūĨŌķÍžĢŽģÉžĻīóÓÚ70·ÖΊĄ°ģÉžĻÓÅÁžĄą.
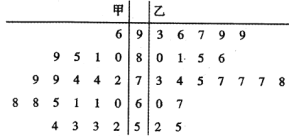
ĢĻ1ĢĐÓÉŌÔÉÏÍģžÆĘýūÝĖîÐīÏÂÃæ![]() ÁÐÁŠąíĢŽēĒÅÐķÏÄÜ·ņÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý
ÁÐÁŠąíĢŽēĒÅÐķÏÄÜ·ņÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý![]() ĩÄĮ°ĖáÏÂČÏΊĄ°ģÉžĻÓÅÁžÓë―ĖŅ§·―Ę―ÓÐđØĄąĢŋ
ĩÄĮ°ĖáÏÂČÏΊĄ°ģÉžĻÓÅÁžÓë―ĖŅ§·―Ę―ÓÐđØĄąĢŋ
žŨ°ā | ŌŌ°ā | ŨÜžÆ | |
ģÉžĻÓÅÁž | |||
ģÉžĻēŧÓÅÁž | |||
ŨÜžÆ |
ĢĻ2ĢĐīÓžŨĄĒŌŌÁ―°ā40ļöŅųąūÖÐĢŽģÉžĻÔÚ60·ÖŌÔÏÂĢĻēŧšŽ60·ÖĢĐĩÄŅ§ÉúÖÐČÎŌâŅĄČĄ2ČËĢŽžĮĀīŨÔžŨ°āĩÄČËĘýΊ![]() ĢŽĮó
ĢŽĮó![]() ĩÄ·ÖēžÁÐÓëĘýŅ§ÆÚÍû.
ĩÄ·ÖēžÁÐÓëĘýŅ§ÆÚÍû.
ļ―Ģš ĢĻÆäÖÐ
ĢĻÆäÖÐ![]() ĢĐ
ĢĐ
|
|
|
|
|
|
|
|
|
|
Ąūīð°ļĄŋĢĻ1ĢĐÁÐÁŠąížû―âÎöĢŽÄÜÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý0.05ĩÄĮ°ĖáÏÂČÏΊĄ°ģÉžĻÓÅÁžÓë―ĖŅ§·―Ę―ÓÐđØĄąĢŧĢĻ2ĢĐ·ÖēžÁОû―âÎöĢŽ![]() .
.
Ąū―âÎöĄŋ
(1)ļųūÝūĨŌķÍžÖÐĩÄĘýūÝĖîÐīÁÐÁŠąí,ČŧšóžÆËã![]() ,ÔŲķÔÕÕąíĩÃģö―áÂÛ;
,ÔŲķÔÕÕąíĩÃģö―áÂÛ;
(2)ÏČČ·ķĻžŨ°āČËĘý![]() ĩÄËųÓÐŋÉÄÜČĄÖĩ,Čŧšó·ÖąðĮóÆäļÅÂĘ,ÔŲĩÃĩ―XĩÄ·ÖēžÁКÍĘýŅ§ÆÚÍû.
ĩÄËųÓÐŋÉÄÜČĄÖĩ,Čŧšó·ÖąðĮóÆäļÅÂĘ,ÔŲĩÃĩ―XĩÄ·ÖēžÁКÍĘýŅ§ÆÚÍû.
―â:(1)ļųūÝūĨŌķÍžÖÐĩÄĘýūÝŨũģö![]() ÁÐÁŠąíČįąíËųĘū,
ÁÐÁŠąíČįąíËųĘū,
žŨ°ā | ŌŌ°ā | ŨÜžÆ | |
ģÉžĻÓÅÁž | 10 | 16 | 26 |
ģÉžĻēŧÓÅÁž | 10 | 4 | 14 |
ŨÜžÆ | 20 | 20 | 40 |
ļųūÝ![]() ÁÐÁŠąíÖÐĩÄĘýūÝ,ĩÃ
ÁÐÁŠąíÖÐĩÄĘýūÝ,ĩÃ![]() ,
,
ËųŌÔÄÜÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý0.05ĩÄĮ°ĖáÏÂČÏΊĄ°ģÉžĻÓÅÁžÓë―ĖŅ§·―Ę―ÓÐđØĄą.
(2)žŨĄĒŌŌÁ―°ā40ļöŅųąūÖÐ,ģÉžĻÔÚ60·ÖŌÔÏÂ(ēŧšŽ60·Ö)ĩÄŅ§ÉúČËĘýΊ6.
ÓÉĖâŌâŋÉÖŠXĩÄČĄÖĩ·ÖąðΊ![]() ,
,![]() ,
,![]() ,Ôō
,Ôō
![]() Ģŧ
Ģŧ![]() Ģŧ
Ģŧ![]() .
.
Ąā![]() ĩÄ·ÖēžÁÐΊ
ĩÄ·ÖēžÁÐΊ
| 0 | 1 | 2 |
|
|
|
|
ÆäĘýŅ§ÆÚÍû![]()
![]() .
.


 ŨīÔŠž°ĩÚÏĩÁÐīð°ļ
ŨīÔŠž°ĩÚÏĩÁÐīð°ļ ÍŽē―°ÂĘýÏĩÁÐīð°ļ
ÍŽē―°ÂĘýÏĩÁÐīð°ļ
| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠĘýÁÐ![]() ĩÄĮ°
ĩÄĮ°![]() ÏîšÍ
ÏîšÍ![]() ÂúŨã
ÂúŨã![]() .
.
(1)ÖĪÃũĘýÁÐ![]() ΊĩČēîĘýÁÐĢŽēĒĮóģöĘýÁÐ
ΊĩČēîĘýÁÐĢŽēĒĮóģöĘýÁÐ![]() ĩÄÍĻÏîđŦĘ―.
ĩÄÍĻÏîđŦĘ―.
(2)ČôēŧĩČĘ―![]() ĢŽķÔČÎŌâ
ĢŽķÔČÎŌâ![]() šãģÉÁĒĢŽĮó
šãģÉÁĒĢŽĮó![]() ĩÄČĄÖĩ·ķΧ.
ĩÄČĄÖĩ·ķΧ.
(3)žĮĘýÁÐ ĩÄĮ°
ĩÄĮ°![]() ÏîšÍΊ
ÏîšÍΊ![]() ĢŽĘĮ·ņīæÔÚÕýÕûĘý
ĢŽĘĮ·ņīæÔÚÕýÕûĘý![]() ĢŽ
ĢŽ![]() ĘđĩÃ
ĘđĩÃ![]() ģÉÁĒĢŽČôīæÔÚĢŽĮóģöËųÓзûšÏĖõžþĩÄÓÐÐōĘĩĘýķÔ(
ģÉÁĒĢŽČôīæÔÚĢŽĮóģöËųÓзûšÏĖõžþĩÄÓÐÐōĘĩĘýķÔ(![]() ĢŽ
ĢŽ![]() )ĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉ.
)ĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠĖÝÐÎABCDĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽPΊČý―ĮÐÎBCDÄÚŌŧĩãĢĻ°üĀĻąß―įĢĐĢŽ
ĢŽPΊČý―ĮÐÎBCDÄÚŌŧĩãĢĻ°üĀĻąß―įĢĐĢŽ![]() ĢŽÔō
ĢŽÔō![]() ĩÄČĄÖĩ·ķΧΊ________.
ĩÄČĄÖĩ·ķΧΊ________.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍžĢŽŌŅÖŠ![]() ĘĮÕýČý―ĮÐÎĢŽEAĢŽCDķžīđÖąÓÚÆ―ÃæABCĢŽĮŌ
ĘĮÕýČý―ĮÐÎĢŽEAĢŽCDķžīđÖąÓÚÆ―ÃæABCĢŽĮŌ![]() ĢŽķþÃæ―Į
ĢŽķþÃæ―Į![]() ĩÄÆ―Ãæ―ĮīóÐĄÎŠ
ĩÄÆ―Ãæ―ĮīóÐĄÎŠ![]() ĢŽFĘĮBEĩÄÖÐĩãĢŽĮóÖĪĢš
ĢŽFĘĮBEĩÄÖÐĩãĢŽĮóÖĪĢš
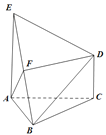
ĢĻ1ĢĐ![]() Æ―ÃæABCĢŧ
Æ―ÃæABCĢŧ
ĢĻ2ĢĐ![]() Æ―ÃæEDBĢŧ
Æ―ÃæEDBĢŧ
ĢĻ3ĢĐĮóžļšÎĖå![]() ĩÄĖåŧý.
ĩÄĖåŧý.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠēŧĩČĘ―|x+1|Ģū|2Đx|+1ĩÄ―âžŊΊMĢŽĮŌaĢŽbĢŽcĄĘMĢŪ
ĢĻ1ĢĐąČ―Ï|aĐb|Óë|1Đab|ĩÄīóÐĄĢŽēĒËĩÃũĀíÓÉĢŧ
ĢĻ2ĢĐČô![]() ĢŽĮóa2+b2+c2ĩÄŨîÐĄÖĩĢŪ
ĢŽĮóa2+b2+c2ĩÄŨîÐĄÖĩĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() .
.
(1)ĖÖÂÛšŊĘý![]() ĩÄĩĨĩũÐÔĢŧ
ĩÄĩĨĩũÐÔĢŧ
(2)ČôđØÓÚ![]() ĩÄ·―ģĖ
ĩÄ·―ģĖ![]() ÓÐÎĻŌŧĘĩĘý―â
ÓÐÎĻŌŧĘĩĘý―â![]() ĢŽĮŌ
ĢŽĮŌ![]() ĢŽĮó
ĢŽĮó![]() ĩÄÖĩ.
ĩÄÖĩ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋČįÍž1ĢŽÔÚĩČŅü![]() ÖÐĢŽ
ÖÐĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ·ÖąðΊ
·ÖąðΊ![]() ĢŽ
ĢŽ![]() ĩÄÖÐĩãĢŽ
ĩÄÖÐĩãĢŽ![]() Ί
Ί![]() ĩÄÖÐĩãĢŽ
ĩÄÖÐĩãĢŽ![]() ÔÚÏßķÎ
ÔÚÏßķÎ![]() ÉÏĢŽĮŌ
ÉÏĢŽĮŌ![]() ĄĢ―Ŧ
ĄĢ―Ŧ![]() ŅØ
ŅØ![]() ÕÛÆðĢŽĘđĩã
ÕÛÆðĢŽĘđĩã![]() ĩ―
ĩ―![]() ĩÄÎŧÖÃĢĻČįÍž2ËųĘūĢĐĢŽĮŌ
ĩÄÎŧÖÃĢĻČįÍž2ËųĘūĢĐĢŽĮŌ![]() ĄĢ
ĄĢ
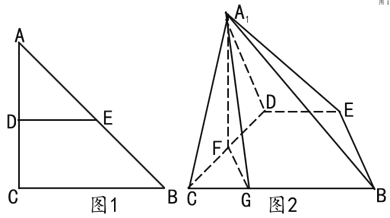
ĢĻ1ĢĐÖĪÃũĢš![]() Æ―Ãæ
Æ―Ãæ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐĮóÆ―Ãæ![]() ÓëÆ―Ãæ
ÓëÆ―Ãæ![]() ËųģÉČņķþÃæ―ĮĩÄÓāÏŌÖĩ
ËųģÉČņķþÃæ―ĮĩÄÓāÏŌÖĩ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠËŦĮúÏß![]() ĩÄÓŌķĨĩãΊAĢŽŌÔAΊÔēÐÄĢŽbΊ°ëūķŨöÔēĢŽÔēAÓëËŦĮúÏßCĩÄŌŧĖõ―Ĩ―üÏßÏā―ŧÓÚMĢŽNÁ―ĩãĢŽČô
ĩÄÓŌķĨĩãΊAĢŽŌÔAΊÔēÐÄĢŽbΊ°ëūķŨöÔēĢŽÔēAÓëËŦĮúÏßCĩÄŌŧĖõ―Ĩ―üÏßÏā―ŧÓÚMĢŽNÁ―ĩãĢŽČô![]() ĢĻ
ĢĻ![]() ΊŨøąęÔĩãĢĐĢŽÔōËŦĮúÏßCĩÄĀëÐÄÂĘΊ___________.
ΊŨøąęÔĩãĢĐĢŽÔōËŦĮúÏßCĩÄĀëÐÄÂĘΊ___________.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘý![]() ĢŽĢĻ
ĢŽĢĻ![]() ĢŽ
ĢŽ![]() ĢĐĢŪ
ĢĐĢŪ
ĢĻ1ĢĐČô![]() ĢŽĮó
ĢŽĮó![]() ĩÄžŦÖĩšÍĩĨĩũĮøžäĢŧ
ĩÄžŦÖĩšÍĩĨĩũĮøžäĢŧ
ĢĻ2ĢĐČôÔÚĮøžä![]() ÉÏÖÁÉŲīæÔÚŌŧĩã
ÉÏÖÁÉŲīæÔÚŌŧĩã![]() ĢŽĘđĩÃ
ĢŽĘđĩÃ![]() ģÉÁĒĢŽĮóĘĩĘýaĩÄČĄÖĩ·ķΧĢŪ
ģÉÁĒĢŽĮóĘĩĘýaĩÄČĄÖĩ·ķΧĢŪ
ēéŋīīð°ļšÍ―âÎö>>
đúžĘŅ§ÐĢÓÅŅĄ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com