
已知数列 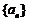 、
、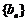 满足
满足  ,
, ,
, 。
。
(I)求证数列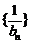 为等差数列,并写出数列
为等差数列,并写出数列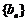 的通项公式;
的通项公式;
(II)若数列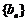 的前
的前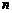 项和为
项和为 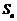 ,设
,设 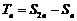 ,求证:
,求证: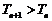 。
。
解:(I)由 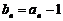 得
得 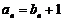 代入
代入 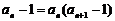 ,
,
得 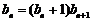 ,整理得
,整理得  。
。
∵ 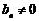 ,
否则
,
否则 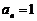 ,与
,与
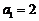 矛盾。
矛盾。
从而得 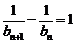 ,
,
∵ 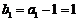 ∴数列
∴数列
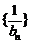 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。
∴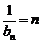 ,即
,即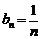 .--------------------------------------------------------------7分
.--------------------------------------------------------------7分
(II)∵ 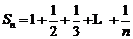 ,
,
∴ 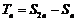 =
=
=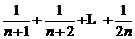 。
。
证法1:∵ 
=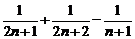
=
∴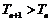 .--------------------------------------------------------------14分
.--------------------------------------------------------------14分
证法2: ∵ 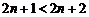 , ∴
, ∴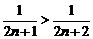 ,
,
∴ 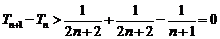 。
。
∴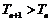 .---------------------------------------------------------------14分
.---------------------------------------------------------------14分
(III)(教师讲评试卷的时候可以选用该小题)
求证:对任意的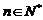 有
有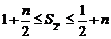 成立.
成立.
用数学归纳法证明:
①当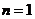 时
时 ,不等式成立;
,不等式成立;
②假设当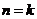 (
(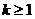 ,
, )时,不等式成立,即
)时,不等式成立,即
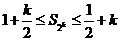 ,那么当
,那么当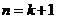 时
时
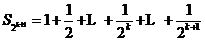
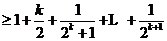
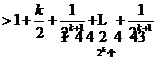
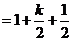
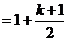
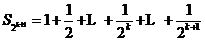
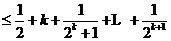
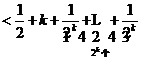
=
∴当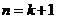 时,不等式成立。
时,不等式成立。
由①②知对任意的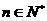 ,不等式成立.
,不等式成立.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
| 9 |
| 10 |
| 1 |
| bn |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com