
如图,长方体 中,
中, ,
, ,点
,点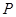 为
为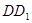 的中点。
的中点。
(1)求证:直线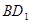 ∥平面
∥平面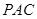 ;
;
(2)求证:平面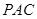
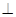 平面
平面 ;
;
(1)详见解析;(2)详见解析.
解析试题分析:(1)设AC与BD的交点为O,连接OP,则长方体中O为BD中点,又P为DD1的中点,所以三角形BDD1中,由中位线定理可知PO ∥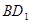 ,根据线面平行的判定定理即可,得证;(2)根据四边形ABCD为菱形,故BD
,根据线面平行的判定定理即可,得证;(2)根据四边形ABCD为菱形,故BD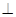 AC,由题意可知DD1
AC,由题意可知DD1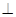 AC,故AC
AC,故AC 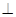 平面
平面 ,进而可证明出结论.
,进而可证明出结论.
解:(1)设AC与BD的交点为O,连接OP,则长方体中O为BD中点,又P为DD1的中点,
所以三角形BDD1中,PO ∥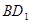 ,而
,而 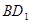 不在平面PAC内,OP在平面PAC内,故
不在平面PAC内,OP在平面PAC内,故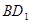 ∥平面
∥平面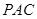
(2)长方体 中,AB=AD,所以ABCD为菱形,故BD
中,AB=AD,所以ABCD为菱形,故BD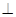 AC,
AC,
又长方体中,DD1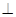 面ABCD,所以DD1
面ABCD,所以DD1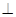 AC,从而AC
AC,从而AC 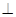 平面
平面 ,则平面
,则平面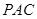
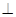 平面
平面
考点:1.线面平行的判定;2.线面垂直的判定;3.面面垂直的判定.


科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.
(1)求证:AD⊥PB;
(2)求点E到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在正方体 中,
中, ,
, 为
为 的中点,
的中点, 为
为 的中点.
的中点.
(1)求证:平面 平面
平面 ;
;
(2)求证: 平面
平面 ;
;
(3)设 为正方体
为正方体 棱上一点,给出满足条件
棱上一点,给出满足条件 的点
的点 的个数,并说明理由.
的个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2014·海淀模拟)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1,且E是BC中点.
(1)求证:A1B∥平面AEC1.
(2)求证:B1C⊥平面AEC1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF= AB,PH为△PAD边上的高.
AB,PH为△PAD边上的高.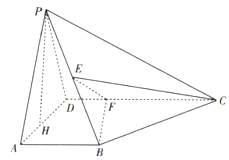
(1)证明:PH⊥平面ABCD;
(2)若PH=1,AD=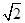 ,FC=1,求三棱锥E-BCF的体积;
,FC=1,求三棱锥E-BCF的体积;
(3)证明:EF⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,长方体 中,
中, ,G是
,G是 上的动点。
上的动点。
(l)求证:平面ADG
 ;
;
(2)判断 与平面ADG的位置关系,并给出证明;
与平面ADG的位置关系,并给出证明;
(3)若G是 的中点,求二面角G-AD-C的大小;
的中点,求二面角G-AD-C的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,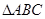 在平面
在平面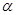 内,
内,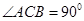 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面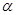 外一个动点,且PC=
外一个动点,且PC=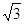 ,
,
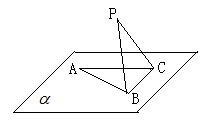
(1)问当PA的长为多少时,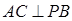
(2)当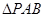 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com