
【题目】已知函数![]() .
.
(1)若![]() 为
为![]() 的极值点,求实数
的极值点,求实数![]() 的值;
的值;
(2)若![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 使方程
使方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)求导![]() 若
若![]() 为
为![]() 的极值点,则
的极值点,则![]() 从而求得结果.(2)由f(x)在[1,+∞)上为增函数,则有f′(x)≥0,x∈[1,+∞)上恒成立求解.若
从而求得结果.(2)由f(x)在[1,+∞)上为增函数,则有f′(x)≥0,x∈[1,+∞)上恒成立求解.若![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上为增函数成立,若
上为增函数成立,若![]() ,
,
![]() 对
对![]() 上恒成立. 对称轴为
上恒成立. 对称轴为![]() ,从而
,从而![]() 在
在![]() 上为增函数. 只要
上为增函数. 只要![]() 即可(3)将a=-1代入,方程f(1x)(1x)3=
即可(3)将a=-1代入,方程f(1x)(1x)3=![]() 可转化为b=xlnx+x2-x3,x>0上有解,只要求得函数g(x)=xlnx+x2-x3的值域即可.
可转化为b=xlnx+x2-x3,x>0上有解,只要求得函数g(x)=xlnx+x2-x3的值域即可.
试题解析:
(1)![]()
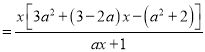
∵![]() 为
为![]() 的极值点,∴
的极值点,∴![]()
∴![]() 且
且![]() ∴
∴![]()
又当![]() 时,
时, ![]() ,从而
,从而![]() 为
为![]() 的极值点成立.
的极值点成立.
(2)因为![]() 在
在![]() 上为增函数,
上为增函数,
所以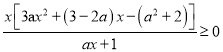 在
在![]() 上恒成立.
上恒成立.
若![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上为增函数成立
上为增函数成立
若![]() ,由
,由![]() 对
对![]() 恒成立知
恒成立知![]() .
.
所以![]() 对
对![]() 上恒成立.
上恒成立.
令![]() ,其对称轴为
,其对称轴为![]() ,
,
因为![]() ,所以
,所以![]() ,从而
,从而![]() 在
在![]() 上为增函数.
上为增函数.
所以只要![]() 即可,即
即可,即![]()
所以![]() 又因为
又因为![]()
(3)若![]() 时,方程
时,方程![]()
可得![]()
即![]() 在
在![]() 上有解
上有解
即求函数![]() 的值域.
的值域.
![]() 令
令![]()
由![]() ∵
∵![]() ∴当
∴当![]() 时,
时, ![]() ,
,
从而![]() 在
在![]() 上为增函数;当
上为增函数;当![]() 时,
时, ![]() ,从而
,从而![]() 在
在![]() 上为减函数.
上为减函数.
∴![]() ,而
,而![]() 可以无穷小.∴
可以无穷小.∴![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的不恒为零的函数,且对于任意实数x,y满足:f(2)=2,f(xy)=xf(y)+yf(x),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),考查下列结论:
(n∈N*),考查下列结论:
①f(1)=1;②f(x)为奇函数;③数列{an}为等差数列;④数列{bn}为等比数列.
以上命题正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的外接圆半径R= ![]() ,角A,B,C的对边分别是a,b,c,且
,角A,B,C的对边分别是a,b,c,且 ![]() =
= ![]()
(1)求角B和边长b;
(2)求S△ABC的最大值及取得最大值时的a,c的值,并判断此时三角形的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的首项为8,Sn是其前n项的和,某同学经计算得S2=20,S3=36,S4=65,后来该同学发现了其中一个数算错了,则该数为( )
A.S1
B.S2
C.S3
D.S4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com