
已知抛物线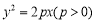 的焦点为双曲线
的焦点为双曲线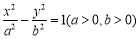 的一个焦点,且两条曲线都经过点
的一个焦点,且两条曲线都经过点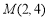 .
.

(1)求这两条曲线的标准方程;
(2)已知点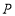 在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点
在抛物线上,且它与双曲线的左,右焦点构成的三角形的面积为4,求点 的坐标.
的坐标.
(1)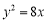 ,
,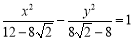 ;(2)
;(2)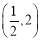 或
或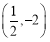 .
.
【解析】
试题分析:(1)可以先利用待定系数法可以先求抛物线方程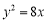 ,然后利用定义法或待定系数法求出双曲线方程
,然后利用定义法或待定系数法求出双曲线方程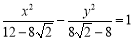 ;
;
(2)先利用三角形的面积是4,求出点p的纵坐标是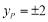 ,再利用点P在抛物线上,求出横坐标
,再利用点P在抛物线上,求出横坐标 即可.
即可.
试题解析:(1)∵抛物线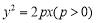 经过点
经过点 ,
,
∴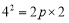 ,解得
,解得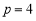 ,
,
∴抛物线的标准方程为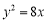 . 3分
. 3分
∴抛物线的焦点为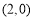 ,∴双曲线的焦点为
,∴双曲线的焦点为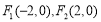 .
.
法一:∴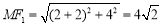 ,
,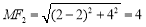 ,
,
∴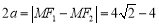 ,
, . 5分
. 5分
∴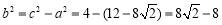 .
.
∴双曲线的标准方程为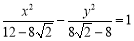 . 8分
. 8分
法二: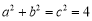 ,∵双曲线经过点
,∵双曲线经过点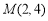 ,∴
,∴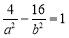 , 5分
, 5分
解得 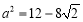 ,
,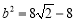 .
.
∴双曲线的标准方程为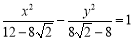 . 8分
. 8分
(2)设点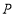 的坐标为
的坐标为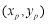 ,由题意得,
,由题意得,
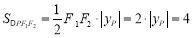 ,∴
,∴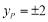 , 11分
, 11分
∵点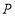 在抛物线上,∴
在抛物线上,∴ ,∴点
,∴点 的坐标为
的坐标为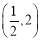 或
或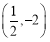 . 14分
. 14分
考点:(1)双曲线的标准方程;(2)抛物线的标准方程.


科目:高中数学 来源:2015届江西新余市高二上学期期末理科A数学试卷(解析版) 题型:选择题
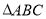 中,
中,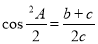 ,则
,则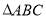 形状是( )
形状是( )
A. 正三角形 B. 直角三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
查看答案和解析>>
科目:高中数学 来源:2015届江苏省常州市高二上学期期末考试理科数学试卷(解析版) 题型:填空题
如图,在正方体 中,点
中,点 在面对角线
在面对角线 上运动,给出下列四个命题:
上运动,给出下列四个命题:

① ∥平面
∥平面 ; ②
; ②  ;
;
③平面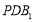 ⊥平面
⊥平面 ;④三棱锥
;④三棱锥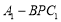 的体
的体
积不变.
则其中所有正确的命题的序号是 .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省常州市高二上学期期末考试文科数学试卷(解析版) 题型:填空题
已知点P在抛物线 上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
上运动,F为抛物线的焦点,点M的坐标为(3,2),当PM+PF取最小值时点P的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com