Question

【题目】已知等差数列{an}满足a4=5，a2+a8=14，数列{bn}满足b1=1，bn+1=2 bn ．
（1）求数列{an}和{bn}的通项公式；
（2）求数列{ }的前n项和；
（3）若cn=an（ ） ，求数列{cn}的前n项和Sn ．

Answer 1

【答案】
（1）解：∵等差数列{an}满足a4=5，a2+a8=14，

∴ ，解得a1=﹣1，d=2，

∴an=2n﹣3．

∵数列{bn}满足b1=1，bn+1=2 bn．

∴ ，∴ ，

以上各式相乘，得 ，

∵b1=1，∴ ．

（2）解：∵ ，

∴数列{ }的前n项和为：

=1﹣ ，

∴ ．

（3）解：∵an=2n﹣3，cn=an（ ） ，

∴ ，

∴ ，①

2Sn=﹣12+122+…+（2n﹣5）2n﹣1+（2n﹣3）2n，②

①﹣②，得 ﹣（2n﹣3）2n

=﹣1+2 ﹣（2n﹣3）2n

=（5﹣2n）2n﹣5，

∴ ．

【解析】（1）由已知条件利用等差数列的通项公式列出方程组求出首项和公差，由此能求出等差数列{an}的通项公式；由已知条件得 ，由此利用累乘法能求出 ．（2）由 ，利用裂项求和法能求出数列{ }的前n项和．（3） ，由此利用错位相减法能求出数列{cn}的前n项和Sn ．
【考点精析】根据题目的已知条件，利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案，需要掌握数列{an}的前n项和sn与通项an的关系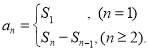；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．