
【题目】某高校在![]() 年的自主招生考试成绩中随机抽取
年的自主招生考试成绩中随机抽取![]() 名学生的笔试成绩,按成绩分组:第
名学生的笔试成绩,按成绩分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() 得到的频率分布直方图如图所示
得到的频率分布直方图如图所示
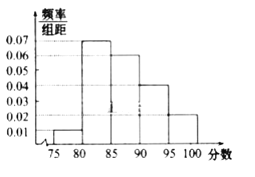
![]() 分别求第
分别求第![]() 组的频率;
组的频率;
![]() 若该校决定在第
若该校决定在第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 名学生进入第二轮面试,
名学生进入第二轮面试,
![]() 已知学生甲和学生乙的成绩均在第
已知学生甲和学生乙的成绩均在第![]() 组,求学生甲和学生乙同时进入第二轮面试的概率;
组,求学生甲和学生乙同时进入第二轮面试的概率;
![]() 根据直方图试估计这
根据直方图试估计这![]() 名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
名学生成绩的平均分.(同一组中的数据用改组区间的中间值代表)
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】给出下列命题:
![]() 用反证法证明命题“设a,b,c为实数,且
用反证法证明命题“设a,b,c为实数,且![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ”时,要给出的假设是:a,b,c都不是正数;
”时,要给出的假设是:a,b,c都不是正数;
![]() 若函数
若函数![]() 在
在![]() 处取得极大值,则
处取得极大值,则![]() 或
或![]() ;
;
![]() 用数学归纳法证明
用数学归纳法证明![]() ,在验证
,在验证![]() 成立时,不等式的左边是
成立时,不等式的左边是![]() ;
;
![]() 数列
数列![]() 的前n项和
的前n项和![]() ,则
,则![]() 是数列
是数列![]() 为等比数列的充要条件;
为等比数列的充要条件;
上述命题中,所有正确命题的序号为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】即将于![]() 年夏季毕业的某大学生准备到贵州非私营单位求职,为了了解工资待遇情况,他在贵州省统计局的官网上,查询到
年夏季毕业的某大学生准备到贵州非私营单位求职,为了了解工资待遇情况,他在贵州省统计局的官网上,查询到![]() 年到
年到![]() 年非私营单位在岗职工的年平均工资近似值(单位:万元),如下表:
年非私营单位在岗职工的年平均工资近似值(单位:万元),如下表:
年份 |
|
|
|
|
|
|
|
|
|
|
序号 |
|
|
|
|
|
|
|
|
|
|
年平均工资 |
|
|
|
|
|
|
|
|
|
|
(1)请根据上表的数据,利用线性回归模型拟合思想,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 的计算结果根据四舍五入精确到小数点后第二位);
的计算结果根据四舍五入精确到小数点后第二位);
(2)如果毕业生对年平均工资的期望值为8.5万元,请利用(1)的结论,预测![]() 年的非私营单位在岗职工的年平均工资(单位:万元。计算结果根据四舍五入精确到小数点后第二位),并判断
年的非私营单位在岗职工的年平均工资(单位:万元。计算结果根据四舍五入精确到小数点后第二位),并判断![]() 年平均工资能否达到他的期望.
年平均工资能否达到他的期望.
参考数据:![]() ,
,![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附:对于一组具有线性相关的数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为

 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若对于函数f(x)=ln(x+1)+x2图象上任意一点处的切线l1,在函数g(x)![]() asin
asin![]() cos
cos![]() x图象上总存在一条切线l2,使得l1⊥l2,则实数a的取值范围为( )
x图象上总存在一条切线l2,使得l1⊥l2,则实数a的取值范围为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月1日,贵阳市地铁一号线全线开通,在一定程度上缓解了出行的拥堵状况.为了了解市民对地铁一号线开通的关注情况,某调查机构在地铁开通后的某两天抽取了部分乘坐地铁的市民作为样本,分析其年龄和性别结构,并制作出如下等高条形图:
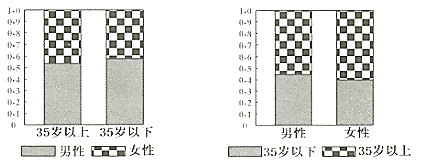
根据图中(![]() 岁以上含
岁以上含![]() 岁)的信息,下列结论中不一定正确的是( )
岁)的信息,下列结论中不一定正确的是( )
A. 样本中男性比女性更关注地铁一号线全线开通
B. 样本中多数女性是![]() 岁以上
岁以上
C. ![]() 岁以下的男性人数比
岁以下的男性人数比![]() 岁以上的女性人数多
岁以上的女性人数多
D. 样本中![]() 岁以上的人对地铁一号线的开通关注度更高
岁以上的人对地铁一号线的开通关注度更高
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽奖活动中,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
共6人获得抽奖机会,抽奖规则如下:若获一等奖后不再参加抽奖,获得二等奖的仍参加三等奖抽奖.现在主办方先从6人中随机抽取2人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖.
(1)求![]() 能获一等奖的概率;
能获一等奖的概率;
(2)若![]() ,
,![]() 已获一等奖,求
已获一等奖,求![]() 能获奖的概率.
能获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,且
上运动,且![]() .
.
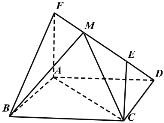
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)设平面![]() 与平面
与平面![]() 所成二面角的大小为
所成二面角的大小为![]() (
(![]() ),求
),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com