
分析 由${S}_{△I{PF}_{1}}$=$\frac{1}{2}$|PF1|•r,S${\;}_{△IP{F}_{2}}$=$\frac{1}{2}$|PF2|•r,S${\;}_{△I{F}_{1}{F}_{2}}$=$\frac{1}{2}$|F1F2|•r,由S${\;}_{△P{F}_{1}{F}_{2}}$=${S}_{△I{PF}_{1}}$+S${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$,根据双曲线的定义2a=$\frac{1}{λ}$×2c,即可求得λ的值.
解答 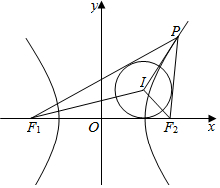 解:由双曲线2x2-y2=2的标准方程:x2-$\frac{{y}^{2}}{2}$=1,a=1,b=$\sqrt{2}$,c=$\sqrt{3}$,依题意,设△PF1F2的内切圆的半径为r,
解:由双曲线2x2-y2=2的标准方程:x2-$\frac{{y}^{2}}{2}$=1,a=1,b=$\sqrt{2}$,c=$\sqrt{3}$,依题意,设△PF1F2的内切圆的半径为r,
则${S}_{△I{PF}_{1}}$=$\frac{1}{2}$|PF1|•r,S${\;}_{△IP{F}_{2}}$=$\frac{1}{2}$|PF2|•r,S${\;}_{△I{F}_{1}{F}_{2}}$=$\frac{1}{2}$|F1F2|•r,
S${\;}_{△P{F}_{1}{F}_{2}}$=${S}_{△I{PF}_{1}}$+S${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$,
由${S}_{△I{PF}_{1}}$+S${\;}_{△IP{F}_{2}}$+S${\;}_{△I{F}_{1}{F}_{2}}$=2S${\;}_{△IP{F}_{2}}$+(1+$\frac{1}{λ}$)S${\;}_{△I{F}_{1}{F}_{2}}$,则${S}_{△I{PF}_{1}}$-S${\;}_{△IP{F}_{2}}$=$\frac{1}{λ}$S${\;}_{△I{F}_{1}{F}_{2}}$,
∴|PF1|-|PF2|=$\frac{1}{λ}$|F1F2|,
∵P为双曲线右支上一点,
∴2a=$\frac{1}{λ}$×2c,则1=$\frac{\sqrt{3}}{λ}$,则λ=$\sqrt{3}$,
∴实数λ的值$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查双曲线的定义、方程和性质,考查三角形的面积公式的运用,运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
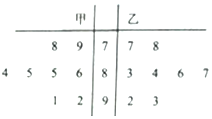 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.
已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (C${\;}_{8}^{3}$+C${\;}_{7}^{2}$)(C${\;}_{7}^{3}$+C${\;}_{8}^{2}$) | B. | (C${\;}_{8}^{3}$+C${\;}_{7}^{2}$)+(C${\;}_{7}^{3}$+C${\;}_{8}^{2}$) | ||
| C. | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$C${\;}_{8}^{2}$ | D. | C${\;}_{8}^{3}$C${\;}_{7}^{2}$+C${\;}_{7}^{3}$+C${\;}_{11}^{1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com