Question

【题目】某制造厂商10月份生产了一批乒乓球，从中随机抽取个进行检查，测得每个球的直径（单位：），将数据进行分组，得到如下频率分布表：

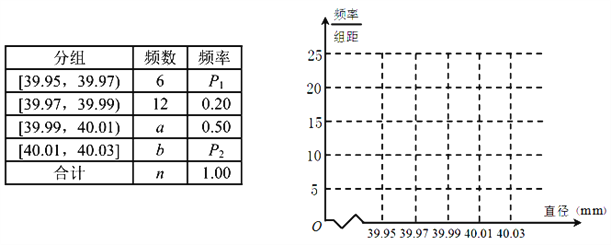
（1）求、、及、的值，并画出频率分布直方图（结果保留两位小数）；

（2）已知标准乒乓球的直径为，且称直径在内的乒乓球为五星乒乓球，若这批乒乓球共有个，试估计其中五星乒乓球的数目；

（3）统计方法中，同一组数据常用该组区间的中点值（例如区间的中点值是）作为代表，试估计这批乒乓球直径的平均值和中位数．

Answer 1

【答案】（1）见解析，（2）5000，（3）平均数为39.996，中位数为．

【解析】

试题分析: （1）根据频率等于频数除以总数，先求总数，再求 对应频数，根据频数和为总数得，最后再根据频率等于频数除以总数，得、的值，以频率除以组距作为对应区间纵坐标画出频率分布直方图，（2）直径在内对应概率为，根据频数等于总数乘以频率，得频数，（3）由平均值为各组中点值与对应概率乘积的和，得平均值；中位数必在区间内，由频率关系列等量关系：设中位数为，则有，解方程可得中位数.

试题解析:（1）由频率分布表可知，，，，.

频率分布直方图如图：

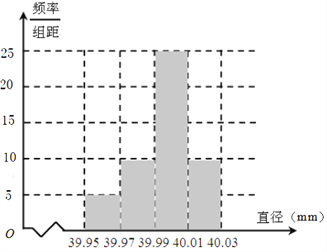
（2）因为五星乒乓球的直径在内，所以由频率分布表，可得五星乒乓球的频率为，（6分）

故个乒乓球中，“五星乒乓球”大约有（个）．

（3）平均数.

设中位数为，则且，解得.故中位数为．