
【题目】已知函数![]() .
.
(I)求f(x)的最小正周期;
(II)求f(x)在区间![]() 上的最小值.
上的最小值.
【答案】【解答】(I)∵![]()
![]() ,
,
∴f(x)的最小正周期为2π
(II)∵![]() ∴
∴![]()
当![]() ,即
,即![]() 时,f(x)取得最小值。
时,f(x)取得最小值。
∴f(x)在区间![]() 上的最小值为
上的最小值为![]() .
.
【解析】本题主要考查倍角公式、两角和的正弦公式、三角函数的周期、三角函数的最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力(I)先利用倍角公式将![]() 降幂,再利用两角和的正弦公式将f(x)化简,使之化简成
降幂,再利用两角和的正弦公式将f(x)化简,使之化简成![]() 的形式,最后利用
的形式,最后利用![]() 计算函数的最小正周期;(II)将X的取值范围代入,先求出
计算函数的最小正周期;(II)将X的取值范围代入,先求出![]() 的范围,再数形结合得到三角函数的最小值,
的范围,再数形结合得到三角函数的最小值,
解题时要注意重要条件“![]() ”,否则很容易出现错误.解本题需要掌握的知识点是降幂公式、辅助角公式、三角函数的最小正周期和三角函数的图象,即
”,否则很容易出现错误.解本题需要掌握的知识点是降幂公式、辅助角公式、三角函数的最小正周期和三角函数的图象,即![]() ,函数
,函数![]() 的最小正周期是
的最小正周期是![]() 。
。
【考点精析】认真审题,首先需要了解三角函数的最值(函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() ).
).


科目:高中数学 来源: 题型:
【题目】(2015·陕西)如图1,在直角梯形ABCD中,AD∥BC,![]() BAD=
BAD=![]() ,AB=BC=1,
,AB=BC=1,
AD=2, E是AD的中点,0是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.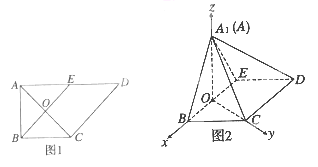
(1)证明:CD⊥平面A1OC
(2)若平面A1BE⊥平面BCDE, 四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015![]() 福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
福建)如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.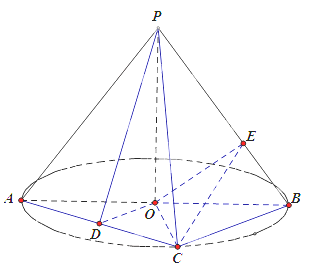
(1)若D为线段AC的中点,求证AC![]() 平面PDO;
平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若BC=![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为![]()
(Ⅰ)求频率分布图中a的值;
(Ⅱ)估计该企业的职工对该部门评分不低于80的概率;
(Ⅲ)从评分在![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在![]() 的概率。
的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,求解下列问题:(1)求
,求解下列问题:(1)求![]() 的单调区间;(2)在锐角 △ A B C 中,角 ∠ A , B , C ,的对边分别为 a , b , c ,若
的单调区间;(2)在锐角 △ A B C 中,角 ∠ A , B , C ,的对边分别为 a , b , c ,若 ![]() = 0 , a = 1 ,求 △ A B C 面积的最大值.
= 0 , a = 1 ,求 △ A B C 面积的最大值.
(1)求![]() 的单调区间;
的单调区间;
(2)在锐角![]() 中,角
中,角![]() ,的对边分别为
,的对边分别为![]() ,若
,若![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加. 现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设![]() 为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件
为事件“选出的4人中恰有2名种子选手,且这2名种子选手来自同一个协会”求事件![]() 发生的概率
发生的概率
(2)设![]() 为选出的4人中种子选手的人数,求随机变量
为选出的4人中种子选手的人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E的方程为![]() +
+![]() =1(a
=1(a![]() b
b![]() 0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足
0),点O为坐标原点,点A的坐标为(a,0),点B的坐标为(0,b),点M在线段AB上,满足![]() =2
=2![]() ,直线OM的斜率为
,直线OM的斜率为![]() 。
。
(1)求E的离心率e。
(2)设点C的坐标为(0,-b),N为线段AC的中点,点N关于直线AB的对称点的纵坐标为![]() ,求E的方程
,求E的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 是双曲线
是双曲线 ![]() 的右焦点,过点
的右焦点,过点 ![]() 作
作 ![]() 的一条渐近线的垂线,垂足为
的一条渐近线的垂线,垂足为 ![]() ,线段
,线段 ![]() 与
与 ![]() 相交于点
相交于点 ![]() ,记点
,记点 ![]() 到
到 ![]() 的两条渐近线的距离之积为
的两条渐近线的距离之积为 ![]() ,若
,若 ![]() ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )
A.![]()
B.2
C. 3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com