
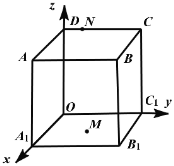
【题目】单位正方体![]() 在空间直角坐标系中的位置如图所示,动点
在空间直角坐标系中的位置如图所示,动点![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,设由
,设由![]() ,
,![]() ,
,![]() 三点确定的平面截该正方体的截面为
三点确定的平面截该正方体的截面为![]() ,那么( )
,那么( )
A.对任意点![]() ,存在点
,存在点![]() 使截面
使截面![]() 为三角形
为三角形
B.对任意点![]() ,存在点
,存在点![]() 使截面
使截面![]() 为正方形
为正方形
C.对任意点![]() 和
和![]() ,截面
,截面![]() 都为梯形
都为梯形
D.对任意点![]() ,存在点
,存在点![]() 使得截面
使得截面![]() 为矩形
为矩形
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的公差为
的公差为![]() ,前n项和为
,前n项和为![]() ,且满足____________.(从①
,且满足____________.(从①![]() );②
);②![]() 成等比数列;③
成等比数列;③![]() ,这三个条件中任选两个补充到题干中的横线位置,并根据你的选择解决问题)
,这三个条件中任选两个补充到题干中的横线位置,并根据你的选择解决问题)
(I)求![]() ;
;
(Ⅱ)若![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为a,线段B1D1上有两个动点E,F,且EF![]() a,以下结论正确的有( )
a,以下结论正确的有( )

A.AC⊥BE
B.点A到△BEF的距离为定值
C.三棱锥A﹣BEF的体积是正方体ABCD﹣A1B1C1D1体积的![]()
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P-ABCD中,底面ABCD为菱形,且![]() ,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.

(1)求证:BG![]() 面PAD;
面PAD;
(2)E是BC的中点,在PC上求一点F,使得PG![]() 面DEF.
面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校![]() 名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共
名学生参加军事冬令营活动,活动期间各自扮演一名角色进行分组游戏,角色按级别从小到大共![]() 种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以
种,分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式,可以![]() 人一组或者
人一组或者![]() 人一组.如果
人一组.如果![]() 人一组,则必须角色相同;如果
人一组,则必须角色相同;如果![]() 人一组,则
人一组,则![]() 人角色相同或者
人角色相同或者![]() 人为级别连续的
人为级别连续的![]() 个不同角色.已知这
个不同角色.已知这![]() 名学生扮演的角色有
名学生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,现在新加入
人,现在新加入![]() 名学生,将这
名学生,将这![]() 名学生分成
名学生分成![]() 组进行游戏,则新加入的学生可以扮演的角色的种数为________.
组进行游戏,则新加入的学生可以扮演的角色的种数为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥PABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分别是AC,PC的中点,F是PB上一点,且
,D,E分别是AC,PC的中点,F是PB上一点,且![]() ,M为PA的中点,二面角
,M为PA的中点,二面角![]() 的大小为45°.
的大小为45°.

(1)证明:![]() 平面AEF;
平面AEF;
(2)求直线AF与平面BCM所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解全市统考情况,从所有参加考试的考生中抽取4000名考生的成绩,频率分布直方图如下图所示.

(1)求这4000名考生的半均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)由直方图可认为考生考试成绩z服从正态分布![]() ,其中
,其中![]() 分别取考生的平均成绩
分别取考生的平均成绩![]() 和考生成绩的方差
和考生成绩的方差![]() ,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
,那么抽取的4000名考生成绩超过84.81分(含84.81分)的人数估计有多少人?
(3)如果用抽取的考生成绩的情况来估计全市考生的成绩情况,现从全市考生中随机抽取4名考生,记成绩不超过84.81分的考生人数为![]() ,求
,求![]() .(精确到0.001)
.(精确到0.001)
附:①![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com