
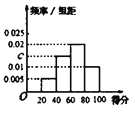
【题目】某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如下:
等级 | 不合格 | 合格 | ||
得分 |
|
|
|
|
频数 | 6 |
| 24 |
|
(1)由该题中频率分布直方图求测试成绩的平均数和中位数;
(2)其他条件不变,在评定等级为“合格”的学生中依次抽取2人进行座谈,每次抽取1人,求在第1次抽取的测试得分低于80分的前提下,第2次抽取的测试得分仍低于80分的概率;
(3)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈.现再从这10人中任选4人,记所选4人的量化总分为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
【答案】(1)64,65;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据频率分布直方图及其性质可求出![]() ,平均数,中位数;
,平均数,中位数;
(2)设“第1次抽取的测试得分低于80分”为事件![]() ,“第2次抽取的测试得分低于80分”为事件
,“第2次抽取的测试得分低于80分”为事件![]() ,由条件概率公式
,由条件概率公式![]() 可求出;
可求出;
(3)从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈,其中“不合格”的学生数为![]() ,“合格”的学生数为6;由题意可得
,“合格”的学生数为6;由题意可得![]() ,5,10,15,20,利用“超几何分布”的计算公式即可得出概率,进而得出分布列与数学期望.
,5,10,15,20,利用“超几何分布”的计算公式即可得出概率,进而得出分布列与数学期望.
由题意知,样本容量为![]() ,
,
![]() .
.
(1)平均数为![]() ,
,
设中位数为![]() ,因为
,因为![]() ,所以
,所以![]() ,则
,则![]() ,
,
解得![]() .
.
(2)由题意可知,分数在![]() 内的学生有24人,分数在
内的学生有24人,分数在![]() 内的学生有12人.设“第1次抽取的测试得分低于80分”为事件
内的学生有12人.设“第1次抽取的测试得分低于80分”为事件![]() ,“第2次抽取的测试得分低于80分”为事件
,“第2次抽取的测试得分低于80分”为事件![]() ,
,
则![]() ,所以
,所以![]() .
.
(3)在评定等级为“合格”和“不合格”的学生中用分层抽样的方法抽取10人,则“不合格”的学生人数为![]() ,“合格”的学生人数为
,“合格”的学生人数为![]() .
.
由题意可得![]() 的所有可能取值为0,5,10,15,20.
的所有可能取值为0,5,10,15,20.
![]() ,
,
![]() .
.
所以![]() 的分布列为
的分布列为
| 0 | 5 | 10 | 15 | 20 |
|
|
|
|
|
|
![]() .
.


科目:高中数学 来源: 题型:
【题目】圆![]() :
:![]() (
(![]() )过点
)过点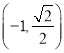 ,离心率为
,离心率为![]() ,其左、右焦点分别为
,其左、右焦点分别为![]() ,
,![]() ,且过焦点
,且过焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,设直线
,设直线![]() 与直线
与直线![]() 的斜率分别为
的斜率分别为![]() ,试证明:
,试证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
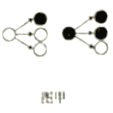
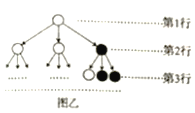
【题目】分形几何学是数学家伯努瓦·曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图:记图乙中第![]() 行黑圈的个数为
行黑圈的个数为![]() ,则(1)
,则(1)![]() _______;(2)
_______;(2)![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民收入逐年增长.某地区2014年至2018年农村居民家庭人均纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
人均纯收入 | 5 | 4 | 7 | 8 | 10 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2014年至2018年该地区农村居民家庭人均纯收入的变化情况,并预测2019年该地区农村居民家庭人均纯收入为多少?
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com