
【题目】当今世界科技迅猛发展,信息日新月异.为增强全民科技意识,提高公众科学素养,某市图书馆开展了以“亲近科技、畅想未来”为主题的系列活动,并对不同年龄借阅者对科技类图书的情况进行了调查.该图书馆从只借阅了一本图书的借阅者中随机抽取100名,数据统计如表:
借阅科技类图书(人) | 借阅非科技类图书(人) | |
年龄不超过50岁 | 20 | 25 |
年龄大于50岁 | 10 | 45 |
(1)是否有99%的把握认为年龄与借阅科技类图书有关?
(2)该图书馆为了鼓励市民借阅科技类图书,规定市民每借阅一本科技类图书奖励积分2分,每借阅一本非科技类图书奖励积分1分,积分累计一定数量可以用积分换购自己喜爱的图书.用表中的样本频率作为概率的估计值.
(i)现有3名借阅者每人借阅一本图书,记此3人增加的积分总和为随机变量ξ,求ξ的分布列和数学期望;
(ii)现从只借阅一本图书的借阅者中选取16人,则借阅科技类图书最有可能的人数是多少?
附:K2![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
【答案】(1)有99%的把握认为年龄与借阅科技类图书有关;(2)(i)分布列详见解析,数学期望为3.9;(ii)5人.
【解析】
(1)根据K2的表达式代入计算即可判断;
(2)(i)由题知借阅科技类图书的概率P![]() ,若这3人增加的积分总和为随机变量ξ,分别计算出P(ξ=3),P(ξ=4),P(ξ=5),P(ξ=6),即可得到分布列及期望;
,若这3人增加的积分总和为随机变量ξ,分别计算出P(ξ=3),P(ξ=4),P(ξ=5),P(ξ=6),即可得到分布列及期望;
(ii)根据题意得随机变量X满足X~B(16,![]() )的二项分布,列出不等式组,解出即可
)的二项分布,列出不等式组,解出即可
解:(1)K2![]() 8.129>6.635,
8.129>6.635,
所以有99%的把握认为年龄与借阅科技类图书有关;
(2)(i)因为用表中的样本频率作为概率的估计值,所以借阅科技类图书的概率P![]() ,
,
因为3名借阅者每人借阅一本图书,这3人增加的积分总和为随机变量ξ,
所以随机变量ξ的可能取值为3,4,5,6,
P(ξ=3)![]()
P(ξ=4)![]()
P(ξ=5)![]()
P(ξ=6)![]() ,
,
从而ξ的分布列为:
ξ | 3 | 4 | 5 | 6 |
P |
|
|
|
|
所以E(ξ)=3![]() 4
4![]() 5
5![]() 6
6![]() 3.9;
3.9;
(ii)记16人中借阅科技类图书的人数为X,则随机变量X满足二项分布X~B(16,![]() )
)
设借阅科技类图书最有可能的人数时k(k=0,1,2,……,16)
则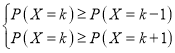 ,
,
而![]() ,
,![]() ,
,
解得4.1≤k≤5.1,
故k=5,
所以16人借阅科技类图书最有可能的人数是5人


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为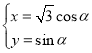 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上位于第一,二象限的两个动点,且
上位于第一,二象限的两个动点,且![]() ,射线
,射线![]() 交曲线
交曲线![]() 分别于
分别于![]() ,求
,求![]() 面积的最小值,并求此时四边形
面积的最小值,并求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某志愿者服务网站在线招募志愿者,当报名人数超过计划招募人数时,将采用随机抽取的方法招募志愿者,如表记录了A,B,C,D四个项目最终的招募情况,其中有两个数据模糊,记为a,b.
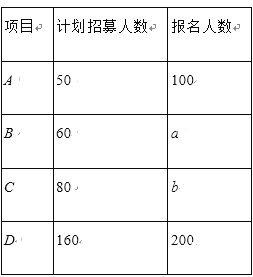
甲同学报名参加了这四个志愿者服务项目,记ξ为甲同学最终被招募的项目个数,已知P(ξ=0)![]() ,P(ξ=4)
,P(ξ=4)![]() .
.
(Ⅰ)求甲同学至多获得三个项目招募的概率;
(Ⅱ)求a,b的值;
(Ⅲ)假设有十名报了项目A的志愿者(不包含甲)调整到项目D,试判断Eξ如何变化(结论不要求证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线C:![]() 1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若
1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若![]() ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻的两条对称轴之间的距离为
,其图像相邻的两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列结论正确的是( ).
对称,则下列结论正确的是( ).
A.函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
B.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
C.若![]() ,则
,则![]() 的值为
的值为![]()
D.要得到函数![]() 的图像,只需要将
的图像,只需要将![]() 的图像向右平移
的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() )的离心率是
)的离心率是![]() ,点
,点![]() 在短轴
在短轴![]() 上,且
上,且![]() 。
。
(1)球椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,过点
为坐标原点,过点![]() 的动直线与椭圆交于
的动直线与椭圆交于![]() 两点。是否存在常数
两点。是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某杂肉观赏区改造建筑用地平面示意图如图所示、经规划调研确定,杂肉观赏区改造规划建筑用地区域是半径为![]() 的圆,该圆面的内接四边形
的圆,该圆面的内接四边形![]() 是原杂肉观赏区建筑用地,测量可知边界
是原杂肉观赏区建筑用地,测量可知边界![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
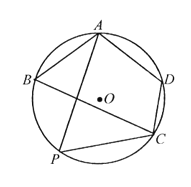
(1)请计算原杂肉观赏区建筑用地![]() 的面积及圆面的半径
的面积及圆面的半径![]() 的值;
的值;
(2)因地理条件的限制,边界![]() 、
、![]() 不能变更,而边界
不能变更,而边界![]() 、
、![]() 可以调整,为了提高杂肉观赏区观赏的时长,请在圆弧
可以调整,为了提高杂肉观赏区观赏的时长,请在圆弧![]() 上设计一点
上设计一点![]() ,使得杂肉观赏区改造的新建筑用地
,使得杂肉观赏区改造的新建筑用地![]() 的周长最大,并求最大值.
的周长最大,并求最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com