
【题目】已知![]() 分别为
分别为![]() 三个内角
三个内角![]() 的对边,且
的对边,且![]() .
.
(1)求![]() ;
;
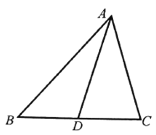
(2)若![]() 为
为![]() 边上的中线,
边上的中线,![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)先由正弦定理将边化为角:![]() ,再根据三角形内角关系消B角:
,再根据三角形内角关系消B角:![]() ,利用两角和正弦公式展开化简得
,利用两角和正弦公式展开化简得![]() ,再利用配角公式得
,再利用配角公式得![]() ,解得
,解得![]() (2)利用向量平行四边形法则得
(2)利用向量平行四边形法则得![]() ,两边平方,根据向量数量积得
,两边平方,根据向量数量积得![]() ;由同角关系得
;由同角关系得![]() ,再由正弦定理可得
,再由正弦定理可得![]() , 解方程组可得
, 解方程组可得![]() ,代入面积公式可得
,代入面积公式可得![]()
试题解析:(1)∵![]() ,由正弦定理得:
,由正弦定理得:
![]() ,即
,即
![]() ,.........................3分
,.........................3分
化简得:![]() ,∴
,∴![]() ..................5分
..................5分
在![]() 中,
中,![]() ,∴
,∴![]() ,得
,得![]() .....................6分
.....................6分
(2)在![]() 中,
中,![]() ,得
,得![]() ...................7分
...................7分
则![]() ........................8分
........................8分
由正弦定理得![]() ............................9分
............................9分
设![]() ,在
,在![]() 中,由余弦定理得:
中,由余弦定理得:
![]() ,则
,则
![]() ,解得
,解得![]() ,
,
即![]() .........................11分
.........................11分
故![]() ........................12分
........................12分


科目:高中数学 来源: 题型:
【题目】经统计,某医院一个结算窗口每天排队结算的人数及相应的概率如下:
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)求每天超过20人排队结算的概率;
(2)求2天中,恰有1天出现超过20人排队结算的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A已知直线![]() 的参数方程为
的参数方程为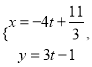 (
(![]() 为参数),在直角坐标系
为参数),在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的方程为
的方程为![]()
(1)求圆![]() 的圆心
的圆心![]() 的极坐标;
的极坐标;
(2)判断直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
![]() 已知不等式
已知不等式![]() 的解集为
的解集为![]()
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①对立事件一定是互斥事件;
②函数![]() 的最小值为2;
的最小值为2;
③八位二进制数能表示的最大十进制数为256;
④在![]() 中,若
中,若![]() ,
, ![]() ,
, ![]() ,则该三角形有两解.
,则该三角形有两解.
其中正确命题的个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com