Question

【题目】设圆x2+y2=12与抛物线x2=4y相交于A，B两点，F为抛物线的焦点，若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点，从左至右依次为P1 ， P2 ， P3 ， P4 ， 则|P1P2|+|P3P4|的值 ， 若直线m与抛物线相交于M，N两点，且与圆相切，切点D在劣弧 上，则|MF|+|NF|的取值范围是 ．

Answer 1

【答案】5 ；[2+4 ，22]
【解析】解：由 ，得 或 ，
即A（﹣2 ，2），B（2 ，2）．
∵点F坐标为（0，1），∴kFB= ，∴kl＞kFB ，
所以直线l与圆交于P1、P3两点，与抛物线交于P2、P4两点，
设P1（x1 ， y1），P2（x2 ， y2），P3（x3 ， y3），P4（x4 ， y4）
把直线l方程：y=x+1代入x2=4y，得x2﹣4x﹣4=0，∴x2+x4=4；
把直线l方程：y=x+1代入x2+y2=12，得2x2+2x﹣11=0，∴x1+x3=﹣1
∴|P1P2|+|P3P4|= [（x2﹣x1）+（x4﹣x3）]= [（x2+x4）﹣（x1+x3）]=5
所以|P1P2|+|P3P4|的值等于5 ．
设直线m的方程为y=k+b（b＞0），
代入抛物线方程得x2﹣4kx﹣4b=0，
设点M（x1 ， y1），N（x2 ， y2），则x1+x2=4k，
则y1+y2=k（x1+x2）+2b=4k2+2b，
∵直线m与该圆相切，∴ = ，即 ，
又|MF|=y1+1，|NF|=y2+1，
∴|MF|+|NF|=y1+y2+2=4k2+2b+2=
∵kOA=﹣ ，kOB= ，∴分别过A、B的圆的切线的斜率为 ，﹣ ．
∴k∈[﹣ ， ]，∴0≤k2≤2，∴0≤ ﹣1≤12，
∵b＞0，∴b∈[2 ，6]
所以|MF|+|NF|的取值范围为[2+4 ，22]．
故答案为：5 ；[2+4 ，22]．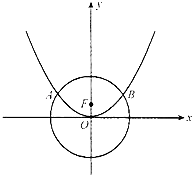

由圆的方程和抛物线的方程联解，求得交点A、B的坐标，从而判断直线l与圆交于P1、P3 ， 直线l与抛物线交于P2、P4 ， 另|P1P2|+|P3+P4|的表达式用P1 ， P2 ， P3 ， P4的四点的横坐标表示，然后根据根与系数的关系，代入表达式，即解；先设直线m的方程y=k+b，交点M、N坐标，再用点M、N纵坐标表示出|MF|+|NF|，由与圆相切，得到k与b的关系，消去k用b表示|MF|+|NF|，即得到关于b的一个函数，由kOA=﹣ ，kOB= ，得到k的范围，由此求得b的范围，再将b的代入|MF|+|NF|的函数关系式中并求出其范围．