
【题目】已知函数![]() .
.
(1)当![]() 时,若
时,若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数a的取值范围;
成立,求实数a的取值范围;
(2)当![]() 时,求x的取值范围.
时,求x的取值范围.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)先利用函数的单调性得当x∈[0,1]时,g(x)∈[1,3],f(x)∈[62a,5],再根据已知得到
[1,3][62a,5],解不等式即得解.(2)先化简得![]() ,再对a分类讨论求x的取值范围.
,再对a分类讨论求x的取值范围.
(1)∵g(x)=2x+log2(x+1)在[0,1]上递增,f(x)在[0,1]上递减,
当x∈[0,1]时,g(x)∈[1,3],f(x)∈[62a,5]
∵对任意的x∈[0,1],都存在![]() ∈[0,1],使得f(
∈[0,1],使得f(![]() )=g(x)成立;
)=g(x)成立;
∴[1,3][62a,5]
∴62a1,
即a![]() .
.
(2)![]()
![]()
![]()
当a=0时,x>1
当a≠0时,①当0<a<1时,1<x<![]()
②当a>1时,![]() <x<1
<x<1
③当a=1时,无解
④当a<0时,x<![]() 或x>1
或x>1
综上所述,当a=0时,x的取值范围为![]()
当a≠0时,①当0<a<1时,x的取值范围为![]()
②当a>1时,x的取值范围为![]()
③当a=1时,无解
④当a<0时,x的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】(1)求过点P(2,3),且在两坐标轴上的截距相等的直线方程.
(2)已知直线l平行于直线4x+3y-7=0,直线l与两坐标轴围成的三角形的周长是15,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln2x-2aln(ex)+3,x∈[e-1,e2]
(1)当a=1时,求函数f(x)的值域;
(2)若f(x)≤-alnx+4恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求二面角A﹣DF﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]() 在第一象限的交点为
在第一象限的交点为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的右顶点,
为椭圆的右顶点, ![]() 的面积为
的面积为![]() .
.
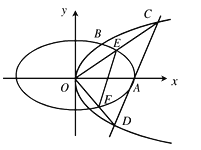
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线
点作直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() 两点,记
两点,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市拟兴建九座高架桥,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
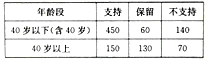
(1)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在40岁以下(含40岁)的人有多少被抽取;
(2)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在40岁以上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点,若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1 , P2 , P3 , P4 , 则|P1P2|+|P3P4|的值 , 若直线m与抛物线相交于M,N两点,且与圆相切,切点D在劣弧 ![]() 上,则|MF|+|NF|的取值范围是 .
上,则|MF|+|NF|的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点F1 , F2其离心率为e=
=1(a>b>0)的左右焦点F1 , F2其离心率为e= ![]() ,点P为椭圆上的一个动点,△PF1F2内切圆面积的最大值为
,点P为椭圆上的一个动点,△PF1F2内切圆面积的最大值为 ![]() .
.
(1)求a,b的值
(2)若A、B、C、D是椭圆上不重合的四个点,且满足 ![]() ,
, ![]() =0,求|
=0,求| ![]() |+|
|+| ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com