
【题目】已知圆![]() ,
, ![]() 是
是![]() 轴上的动点
轴上的动点![]() 分别切圆
分别切圆![]() 于
于![]() 两点.
两点.
(1)若![]() ,求切线
,求切线![]() 的方程;
的方程;
(2)若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() 的方程分别为
的方程分别为![]() 和
和![]()
(2) ![]() 的方程为
的方程为![]() 或
或![]()
【解析】试题分析:(1)设出切线方程,利用圆心到直线的距离列出方程求解即可:(2)设![]() 与
与![]() 交于点
交于点![]() ,求出
,求出![]() ,利用相似三角形,
,利用相似三角形, ![]() ,设
,设![]() ,通过
,通过![]() ,求解即可.
,求解即可.
试题解析:(1)设过点Q的圆M的切线方程为x=my+1,则圆心M到切线的距离为1,
∴![]() =1,∴m=-
=1,∴m=-![]() 或0,∴
或0,∴ ![]() 的方程分别为
的方程分别为![]() 和
和![]() ...6分
...6分
(2)设AB与MQ交于P,则MP⊥AB,MB⊥BQ,∴|MP|=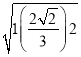 =
=![]() .在Rt△MBQ中,|MB|2=|MP||MQ|,
.在Rt△MBQ中,|MB|2=|MP||MQ|,
即1=![]() |MQ|,∴|MQ|=3,∴x2+(y-2)2=9.设Q(x,0),则x2+22=9,∴x=±
|MQ|,∴|MQ|=3,∴x2+(y-2)2=9.设Q(x,0),则x2+22=9,∴x=±![]() ,∴Q(±
,∴Q(±![]() ,0),∴
,0),∴ ![]() 的方程为
的方程为![]() 或
或![]()


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
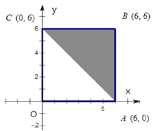
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:3x+2y﹣1=0和l2:5x+2y+1=0的交点为A
(1)若直线l3:(a2﹣1)x+ay﹣1=0与l1平行,求实数a的值;
(2)求经过点A,且在两坐标轴上截距相等的直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an+1= ![]() an+t,a1=
an+t,a1= ![]() (t为常数,且t≠
(t为常数,且t≠ ![]() ).
).
(1)证明:{an﹣2t}为等比数列;
(2)当t=﹣ ![]() 时,求数列{an}的前几项和最大?
时,求数列{an}的前几项和最大?
(3)当t=0时,设cn=4an+1,数列{cn}的前n项和为Tn , 若不等式 ![]() ≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
≥2n﹣7对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程![]() ,其左焦点、上顶点和左顶点分别为
,其左焦点、上顶点和左顶点分别为![]() ,
, ![]() ,
, ![]() ,坐标原点为
,坐标原点为![]() ,且线段
,且线段![]() ,
, ![]() ,
, ![]() 的长度成等差数列.
的长度成等差数列.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若过点![]() 的一条直线
的一条直线![]() 交椭圆于点
交椭圆于点![]() ,
, ![]() ,交
,交![]() 轴于点
轴于点![]() ,使得线段
,使得线段![]() 被点
被点![]() ,
, ![]() 三等分,求直线
三等分,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处. 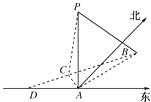
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com