
【题目】已知函数![]()
![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线在y轴上的截距为
处的切线在y轴上的截距为![]() .
.
(1)求a;
(2)讨论函数![]()
![]() 和
和![]()
![]() 的单调性;
的单调性;
(3)设![]()
![]() ,求证:
,求证:![]()
![]() .
.
【答案】(1)![]() (2)
(2)![]()
![]() 为减函数,
为减函数,![]()
![]() 为增函数. (3)证明见解析
为增函数. (3)证明见解析
【解析】
(1)求出导函数![]() ,求出切线方程,令
,求出切线方程,令![]() 得切线的纵截距,可得
得切线的纵截距,可得![]() (必须利用函数的单调性求解);
(必须利用函数的单调性求解);
(2)求函数的导数,由导数的正负确定单调性;
(3)不等式![]() 变形为
变形为![]() ,由
,由![]() 递减,得
递减,得![]() (
(![]() ),即
),即![]() ,即
,即![]() ,依次放缩,
,依次放缩,![]() .
.
不等式![]() ,
,![]() 递增得
递增得![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() ,先证
,先证![]() ,然后同样放缩得出结论.
,然后同样放缩得出结论.
解:(1)对![]() 求导,得
求导,得![]() .
.
因此![]() .又因为
.又因为![]() ,
,
所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() ,
,
即![]() .
.
由题意,![]() .
.
显然![]() ,适合上式.
,适合上式.
令![]()
![]() ,
,
求导得![]() ,
,
因此![]() 为增函数:故
为增函数:故![]() 是唯一解.
是唯一解.
(2)由(1)可知,![]()
![]()
![]()
![]() ,
,
因为![]() ,
,
所以![]()
![]() 为减函数.
为减函数.
因为![]()
![]() ,
,
所以![]()
![]() 为增函数.
为增函数.
(3)证明:由![]()
![]() ,易得
,易得![]() .
.
![]()
由(2)可知,![]()
![]() 在
在![]() 上为减函数.
上为减函数.
因此,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,得
,得![]() ,即
,即![]() .
.
因此,当![]() 时,
时,![]()
![]() .
.
所以![]() 成立.
成立.
下面证明:![]() .
.
由(2)可知,![]()
![]() 在
在![]() 上为增函数.
上为增函数.
因此,当![]() 时,
时,![]() ,
,
即![]() .
.
因此![]() ,
,
即![]() .
.
令![]() ,得
,得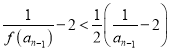 ,
,
即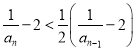 .
.
当![]() 时,
时,
![]()
![]()
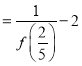
![]() .
.
因为![]() ,
,
所以![]() ,所以
,所以![]() .
.
所以,当![]() 时,
时,
 .
.
所以,当![]() 时,
时,![]() 成立.
成立.
综上所述,当![]() 时,
时,![]() 成立.
成立.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地对产品进行抽查检测,现对某条生产线上随机抽取的100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
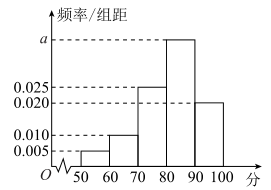
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,视频率作为概率,在该条生产线中随机抽取3个产品,求所抽取的产品中一等品数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 是定义域为
是定义域为![]() 的奇函数,且它的最小正周期是T,已知
的奇函数,且它的最小正周期是T,已知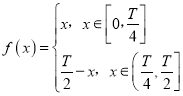 ,
,![]() .给出下列四个判断:①对于给定的正整数
.给出下列四个判断:①对于给定的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 成立;②当a
成立;②当a![]() 时,对于给定的正整数
时,对于给定的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 成立;③当
成立;③当![]()
![]() 时,函数
时,函数![]() 既有对称轴又有对称中心;④当
既有对称轴又有对称中心;④当![]()
![]() 时,
时,![]() 的值只有0或
的值只有0或![]() .其中正确判断的有( )
.其中正确判断的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣sinx+ax(a>0).
(1)若a=1,求证:当x∈(1,![]() )时,f(x)<2x﹣1;
)时,f(x)<2x﹣1;
(2)若f(x)在(0,2π)上有且仅有1个极值点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《周髀算经》中,把圆及其内接正方形称为圆方图,把正方形及其内切圆称为方圆图.圆方图和方圆图在我国古代的设计和建筑领域有着广泛的应用.山西应县木塔是我国现存最古老、最高大的纯木结构楼阁式建筑,它的正面图如图所示.以该木塔底层的边![]() 作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点
作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点![]() 正好位于塔身和塔顶的分界.经测量发现,木塔底层的边
正好位于塔身和塔顶的分界.经测量发现,木塔底层的边![]() 不少于
不少于![]() 米,塔顶
米,塔顶![]() 到点
到点![]() 的距离不超过
的距离不超过![]() 米,则该木塔的高度可能是(参考数据:
米,则该木塔的高度可能是(参考数据:![]() )( )
)( )

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用四种不同颜色给图中的A,B,C,D,E,F六个点涂色,要求每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色,则不同的涂色方法用
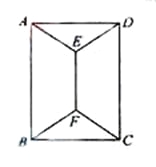
A.288种B.264种C.240种D.168种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,有下述四个结论:
,有下述四个结论:
①![]() 是周期为
是周期为![]() 的函数;
的函数;
②![]() 在
在![]() 单调递增;
单调递增;
③![]() 在
在![]() 上有三个零点;
上有三个零点;
④![]() 的值域是
的值域是![]() .
.
其中所有正确结论的编号是( )
A.②③B.①③C.①③④D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com