
【题目】关于函数![]() ,有下述四个结论:
,有下述四个结论:
①![]() 是周期为
是周期为![]() 的函数;
的函数;
②![]() 在
在![]() 单调递增;
单调递增;
③![]() 在
在![]() 上有三个零点;
上有三个零点;
④![]() 的值域是
的值域是![]() .
.
其中所有正确结论的编号是( )
A.②③B.①③C.①③④D.①②④
【答案】B
【解析】
①计算![]() ,即可判断出结果;②分
,即可判断出结果;②分![]() ,
,![]() 两种情况讨论,根据二次函数以及正弦函数的单调性,即可判断出结果;③分
两种情况讨论,根据二次函数以及正弦函数的单调性,即可判断出结果;③分![]() ,
,![]() 两种情况,分别计算零点,即可判断出结果;④由③,只需计算出
两种情况,分别计算零点,即可判断出结果;④由③,只需计算出![]() 时
时![]() 的最小值,即可判断出结果.
的最小值,即可判断出结果.
①因为![]() ,
,
所以![]() ;
;
因此![]() 是周期为
是周期为![]() 的函数;故①正确;
的函数;故①正确;
②当![]() 时,
时,![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上单调递增,所以
上单调递增,所以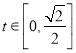 ,
,
又![]() 是开口向上,对称轴为
是开口向上,对称轴为![]() 的二次函数,
的二次函数,
因此![]() 在
在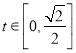 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() 在
在![]() 上单调递增,所以
上单调递增,所以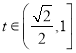 ,
,
又![]() 是开口向下,对称轴为
是开口向下,对称轴为![]() 的二次函数,
的二次函数,
因此![]() 在
在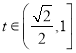 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 上单调递减;故②错;
上单调递减;故②错;
③当![]() 时,
时,![]() ,则
,则![]() ,
,
由![]() ,解得:
,解得:![]() 或
或![]() ,
,
因此![]() 或
或![]() ;
;
当![]() 时,
时,![]() ,则
,则![]()
由![]() ,解得:
,解得:![]() 或
或![]() ,
,
因此![]() ;
;
综上,![]() 在
在![]() 上有三个零点,故③正确;
上有三个零点,故③正确;
④由③可得,当![]() 时,
时,![]() ,
,
令![]() ,根据正弦函数的性质,可得:
,根据正弦函数的性质,可得:
![]() 时,
时, ,
,
又![]() 是开口向上,对称轴为
是开口向上,对称轴为![]() 的二次函数,
的二次函数,
所以![]() ,
,
即![]() 在
在![]() 上的最小值为
上的最小值为![]() ,故④错.
,故④错.
故选:B.


科目:高中数学 来源: 题型:
【题目】![]() 指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当
指数是用体重公斤数除以身高米数的平方得出的数字,是国际上常用的衡量人体胖瘦程度以及是否健康的一个标准.对于高中男体育特长生而言,当![]() 数值大于或等于20.5时,我们说体重较重,当
数值大于或等于20.5时,我们说体重较重,当![]() 数值小于20.5时,我们说体重较轻,身高大于或等于
数值小于20.5时,我们说体重较轻,身高大于或等于![]() 我们说身高较高,身高小于170cm我们说身高较矮.
我们说身高较高,身高小于170cm我们说身高较矮.
(Ⅰ)已知某高中共有32名男体育特长生,其身高与![]() 指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有
指数的数据如散点图,请根据所得信息,完成下述列联表,并判断是否有![]() 的把握认为男生的身高对
的把握认为男生的身高对![]() 指数有影响.
指数有影响.
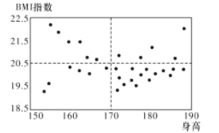
身高较矮 | 身高较高 | 合计 | |
体重较轻 | |||
体重较重 | |||
合计 |
(Ⅱ)①从上述32名男体育特长生中随机选取8名,其身高和体重的数据如表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
体重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根据最小二乘法的思想与公式求得线性回归方程为![]() .利用已经求得的线性回归方程,请完善下列残差表,并求
.利用已经求得的线性回归方程,请完善下列残差表,并求![]() (解释变量(身高)对于预报变量(体重)变化的贡献值)(保留两位有效数字);
(解释变量(身高)对于预报变量(体重)变化的贡献值)(保留两位有效数字);
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
体重(kg) | 58 | 53 | 61 | 66 | 57 | 50 | 66 | |
残差 |
|
|
|
|
|
|
|
②通过残差分析,对于残差的最大(绝对值)的那组数据,需要确认在样本点的采集中是否有人为的错误,已知通过重新采集发现,该组数据的体重应该为![]() .小明重新根据最小二乘法的思想与公式,已算出
.小明重新根据最小二乘法的思想与公式,已算出![]() ,请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.
,请在小明所算的基础上求出男体育特长生的身高与体重的线性回归方程.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: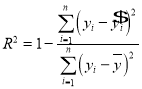 ,
,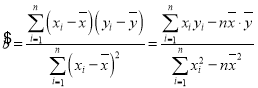 ,
,![]() ,
,![]() ,
,![]() .
.
| 0.10 | 0.05 | 0.01 | 0.005 |
| 2.706 | 3.811 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为实现2020年全面建设小康社会,某地进行产业的升级改造.经市场调研和科学研判,准备大规模生产某高科技产品的一个核心部件,目前只有甲、乙两种设备可以独立生产该部件.如图是从甲设备生产的部件中随机抽取400件,对其核心部件的尺寸x,进行统计整理的频率分布直方图.
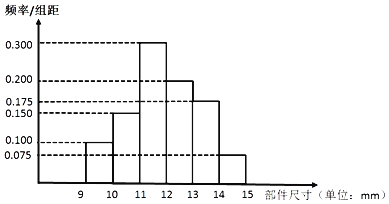
根据行业质量标准规定,该核心部件尺寸x满足:|x﹣12|≤1为一级品,1<|x﹣12|≤2为二级品,|x﹣12|>2为三级品.
(Ⅰ)现根据频率分布直方图中的分组,用分层抽样的方法先从这400件样本中抽取40件产品,再从所抽取的40件产品中,抽取2件尺寸x∈[12,15]的产品,记ξ为这2件产品中尺寸x∈[14,15]的产品个数,求ξ的分布列和数学期望;
(Ⅱ)将甲设备生产的产品成箱包装出售时,需要进行检验.已知每箱有100件产品,每件产品的检验费用为50元.检验规定:若检验出三级品需更换为一级或二级品;若不检验,让三级品进入买家,厂家需向买家每件支付200元补偿.现从一箱产品中随机抽检了10件,结果发现有1件三级品.若将甲设备的样本频率作为总体的慨率,以厂家支付费用作为决策依据,问是否对该箱中剩余产品进行一一检验?请说明理由;
(Ⅲ)为加大升级力度,厂家需增购设备.已知这种产品的利润如下:一级品的利润为500元/件;二级品的利润为400元/件;三级品的利润为200元/件.乙种设备产品中一、二、三级品的概率分别是![]() ,
,![]() ,
,![]() .若将甲设备的样本频率作为总体的概率,以厂家的利润作为决策依据.应选购哪种设备?请说明理由.
.若将甲设备的样本频率作为总体的概率,以厂家的利润作为决策依据.应选购哪种设备?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照水果市场的需要等因素,水果种植户把某种成熟后的水果按其直径![]() 的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
的大小分为不同等级.某商家计划从该种植户那里购进一批这种水果销售.为了了解这种水果的质量等级情况,现随机抽取了100个这种水果,统计得到如下直径分布表(单位:mm):
d |
|
|
|
|
|
等级 | 三级品 | 二级品 | 一级品 | 特级品 | 特级品 |
频数 | 1 | m | 29 | n | 7 |
用分层抽样的方法从其中的一级品和特级品共抽取6个,其中一级品2个.
(1)估计这批水果中特级品的比例;
(2)已知样本中这批水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果待售,商家提出两种收购方案:
方案A:以6.5元/斤收购;
方案B:以级别分装收购,每袋20个,特级品8元/袋,一级品5元/袋,二级品4元/袋,三级品3元/袋.
用样本的频率分布估计总体分布,问哪个方案种植户的收益更高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,将曲线
为参数,将曲线![]() 经过伸缩变换
经过伸缩变换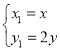 后得到曲线
后得到曲线![]() .在以原点为极点,
.在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,又直线
上的任意一点,又直线![]() 上有两点
上有两点![]() 和
和![]() ,且
,且![]() ,又点
,又点![]() 的极角为
的极角为![]() ,点
,点![]() 的极角为锐角.求:
的极角为锐角.求:
①点![]() 的极角;
的极角;
②![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年12月18日上午10时,在人民大会堂举行了庆祝改革开放40周年大会.40年众志成城,40年砥砺奋进,40年春风化雨,中国人民用双手书写了国家和民族发展的壮丽史诗.会后,央视媒体平台,收到了来自全国各地的纪念改革开放40年变化的老照片,并从众多照片中抽取了100张照片参加“改革开放40年图片展”,其作者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位作者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,作者年龄X服从正态分布![]() ,其中
,其中![]() 近似为样本平
近似为样本平
均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)利用该正态分布,求![]() ;
;
(ii)央视媒体平台从年龄在![]() 和
和![]() 的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“纪念改革开放40年图片展”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是Y,求变量Y的分布列和数学期望.附:
的人数是Y,求变量Y的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,椭圆
,椭圆![]() 上的点到其左焦点
上的点到其左焦点![]() 的最大距离为
的最大距离为![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线与直线
的垂线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最小值和此时直线
的最小值和此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com