
【题目】若点![]() 为点
为点![]() 在平面
在平面![]() 上的正投影,则记
上的正投影,则记![]() .如图,在棱长为
.如图,在棱长为![]() 的正方体
的正方体![]() 中,记平面
中,记平面![]() 为
为![]() ,平面
,平面![]() 为
为![]() ,点
,点![]() 是棱
是棱![]() 上一动点(与
上一动点(与![]() 、
、![]() 不重合)
不重合)![]() ,
,![]() .给出下列三个结论:
.给出下列三个结论:
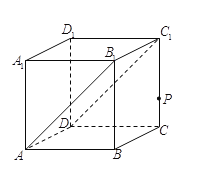
①线段![]() 长度的取值范围是
长度的取值范围是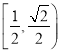 ;
;
②存在点![]() 使得
使得![]() 平面
平面![]() ;
;
③存在点![]() 使得
使得![]() .
.
其中,所有正确结论的序号是( )
A.①②③B.②③C.①③D.①②
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD,E,F分别为AB,CD的中点,将△ADE沿DE折起,使△ACD为等边三角形,如图所示,记二面角A-DE-C的大小为![]() .
.
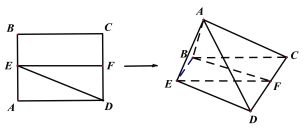
(1)证明:点A在平面BCDE内的射影G在直线EF上;
(2)求角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店投入38万元经销某种纪念品,经销时间共60天,为了获得更多的利润,商店将每天获得的利润投入到次日的经营中,市场调研表明,该商店在经销这第一产品期间第![]() 天的利润
天的利润 (单位:万元,
(单位:万元,![]() ),记第
),记第![]() 天的利润率
天的利润率![]() ,例如
,例如![]() .
.
(1)求![]() 的值;
的值;
(2)求第![]() 天的利润率
天的利润率![]() ;
;
(3)该商店在经销此纪念品期间,哪一天的利润率最大?并求该天的利润率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
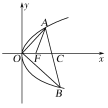
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,![]() (其中O为坐标原点),则△ABO与△AFO面积之和的最小值是________.
(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】业界称“中国芯”迎来发展和投资元年,某芯片企业准备研发一款产品,研发启动时投入资金为A(A为常数)元,之后每年会投入一笔研发资金,n年后总投入资金记为![]() ,经计算发现当
,经计算发现当![]() 时,
时,![]() 近似地满足
近似地满足![]() ,其中
,其中![]() ,
,![]() 为常数,
为常数,![]() .已知3年后总投入资金为研发启动是投入资金的3倍,问:
.已知3年后总投入资金为研发启动是投入资金的3倍,问:
(1)研发启动多少年后,总投入资金是研发启动时投入资金的8倍;
(2)研发启动后第几年投入的资金最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)若![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() ;
;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com