
【题目】已知![]() 在区间
在区间![]() 上的值域
上的值域![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数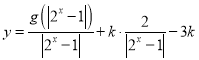 有三个零点,求实数
有三个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:
(1)根据函数![]() 图象的开口方向及对称轴与区间
图象的开口方向及对称轴与区间![]() 的关系得到函数的最值后,根据条件可得
的关系得到函数的最值后,根据条件可得![]() .(2)由已知可得
.(2)由已知可得![]() 在
在![]() 上恒成立,
上恒成立,
分离参数可得![]() 在
在![]() 上恒成立,换元令
上恒成立,换元令![]() ,则
,则![]() ,可得
,可得![]() 在
在![]() 上恒成立,构造函数得到
上恒成立,构造函数得到![]() 的最小值为
的最小值为![]() .(3)由题意可得方程
.(3)由题意可得方程![]() 有三个不同的根,令
有三个不同的根,令![]() ,则得
,则得![]() ,根据函数有3个零点可得方程
,根据函数有3个零点可得方程![]() 有两个不同的实数解
有两个不同的实数解![]() ,且
,且![]() ,或
,或![]() .然后根据方程根的分布得到不等式可得所求范围.
.然后根据方程根的分布得到不等式可得所求范围.
试题解析:
(1)由题意得![]() ,在区间
,在区间![]() 上值域
上值域![]() .
.
①当![]() 时,
时,
则![]() 的最小值为
的最小值为![]() ,
,
由![]() ,解得
,解得![]() ,
,
∴![]() ,
,
此时![]() ,满足在区间
,满足在区间![]() 上值域
上值域![]() .
.
②当![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则![]() 的最小值为
的最小值为![]() ,
,
由![]() ,解得
,解得![]() ,不合题意,舍去.
,不合题意,舍去.
③当![]() 则
则![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则![]() 的最小值为
的最小值为![]() ,
,
由![]() ,解得
,解得![]() .不合题意,舍去.
.不合题意,舍去.
综上![]() .
.
(2)由已知可得![]() 在
在![]() 上恒成立,
上恒成立,
可得化为![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
因![]() ,故
,故![]() ,
,
则![]() 在
在![]() 上恒成立,
上恒成立,
记![]() ,
, ![]() ,
,
故![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() ,
,
故![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.
(3)由题意得函数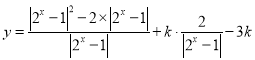 有三个零点,
有三个零点,
故方程![]() 有三个不同的根,
有三个不同的根,
令![]() ,
, ![]() ,
,
∵![]() ,
,
∴当![]() 时,
时, ![]() 的范围
的范围![]() 且单调递减;
且单调递减;
当![]() 时
时![]() 的范围
的范围![]() 且单调递增;
且单调递增;
当![]() 时
时![]() ,
,
当![]() 时
时![]() 的范围
的范围![]() 且单调递增.
且单调递增.
则![]() 有两个不同的实数解
有两个不同的实数解![]() ,
,
已知函数3个零点等价于其中![]() ,或
,或![]() .
.
记![]() ,
,
则![]() ① 或
① 或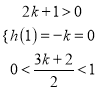 ②
②
解不等组①,得![]() ,而不等式组②无实数解,
,而不等式组②无实数解,
所以实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,设二次函数
中,设二次函数![]() 的图像与两坐标轴有三个交点,经过这三点的圆记为
的图像与两坐标轴有三个交点,经过这三点的圆记为![]()
(1)求圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交,所截得的弦长为4,求直线
相交,所截得的弦长为4,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)函数![]() 若存在
若存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数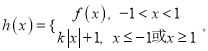 讨论函数
讨论函数![]() 的零点个数(直接写出答案,不要求写出解题过程).
的零点个数(直接写出答案,不要求写出解题过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下面材料:
根据两角和与差的正弦公式,有
![]() ------①
------①
![]() ------②
------②
由①+② 得![]() ------③
------③
令![]() 有
有![]()
代入③得![]() .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:
![]() ;
;
(Ⅱ)若![]() 的三个内角
的三个内角![]() 满足
满足![]() ,试判断
,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 ![]() =λ(0<λ<1).
=λ(0<λ<1).
(Ⅰ)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(Ⅱ)当λ为何值时,平面BEF⊥平面ACD?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点的椭圆 ![]() 的长轴的一个端点是抛物线
的长轴的一个端点是抛物线 ![]() 的焦点,且椭圆
的焦点,且椭圆 ![]() 的离心率是
的离心率是 ![]() .
.
(1)求椭圆 ![]() 的方程;
的方程;
(2)过点 ![]() 的动直线与椭圆
的动直线与椭圆 ![]() 相交于
相交于 ![]() 两点.若线段
两点.若线段 ![]() 的中点的横坐标是
的中点的横坐标是 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() ),其中0<ω<3,已知f(
),其中0<ω<3,已知f( ![]() )=0.
)=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣ ![]() ,
, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y=ax2(a>0)的焦点到准线的距离为 ![]() ,且C上的两点A(x1 , y1),B(x2 , y2)关于直线y=x+m对称,并且
,且C上的两点A(x1 , y1),B(x2 , y2)关于直线y=x+m对称,并且 ![]() ,那么m= .
,那么m= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com