在等比数列{an}中,an>0(n∈N*),且a1a3=4,a3+1是a2和a4的等差中项.
(I)求数列{an}的通项公式;
(II)若数列{bn}满足bn=an+1+log2an(n=1,2,3…),求数列{bn}的前n项和Sn.
解:(I)设等比数列{a
n}的公比为q.
由a
1a
3=4可得a
22=4,(1分)
因为a
n>0,所以a
2=2(2分)
依题意有a
2+a
4=2(a
3+1),得2a
3=a
4=a
3q(3分)
因为a
3>0,所以,q=2..(4分)
所以数列{a
n}通项为a
n=2
n-1(6分)
(II)b
n=a
n+1+log
2a
n=2
n+n-1(18分)
可得
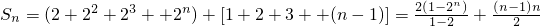
(12分)
=
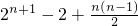
(13分)
分析:(I)求数列{a
n}的通项公式,设出公比为q,由a
1a
3=4,a
3+1是a
2和a
4的等差中项,这两个方程联立即可求出首项与公比,通项易求.
(II)若数列{b
n}满足b
n=a
n+1+log
2a
n(n=1,2,3…),由(I)知求数列{b
n}的前n项和S
n要用分组求和的技巧.
点评:本题考点是等差数列与等比数列的综合,考查等比数列的通项公式、等差数列的性质以及分组求和的技巧,以及根据题设条件选择方法的能力.

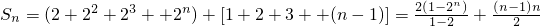 (12分)
(12分)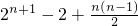 (13分)
(13分)

 名校课堂系列答案
名校课堂系列答案