
【题目】一张坐标纸上涂着圆E: ![]() 及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
及点P(1,0),折叠此纸片,使P与圆周上某点P'重合,每次折叠都会留下折痕,设折痕与直线EP'交于点M .
(1)求 ![]() 的轨迹
的轨迹 ![]() 的方程;
的方程;
(2)直线 ![]() 与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若
与C的两个不同交点为A , B , 且l与以EP为直径的圆相切,若 ![]() ,求△ABO的面积的取值范围.
,求△ABO的面积的取值范围.
【答案】
(1)解:折痕为PP′的垂直平分线,则|MP|=|MP′|,由题意知圆E的半径为2 ![]() ,
,
∴|ME|+|MP|=|ME|+|MP′|=2 ![]() >|EP|,
>|EP|,
∴E的轨迹是以E、P为焦点的椭圆,且a= ![]() ,c=1,
,c=1,
∴b2=a2﹣c2=1, ∴M的轨迹C的方程为 ![]()
(2)解:l与以EP为直径的圆x2+y2=1相切,
则O到l即直线AB的距离: ![]() =1,即m2=k2+1,
=1,即m2=k2+1,
由 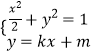 ,消去y , 得(1+2k2)x2+4kmx+2m2﹣2=0,
,消去y , 得(1+2k2)x2+4kmx+2m2﹣2=0,
∵直线l与椭圆交于两个不同点,
∴△=16k2m2﹣8(1+2k2)(m2﹣1)=8k2>0,k2>0,
设A(x1 , y1),B(x2 , y2),则 ![]() ,
, ![]() ,
,
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2= ![]() ,
,
又 ![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,![]()
= ![]() =
= ![]() ,
,
设μ=k4+k2 , 则 ![]() ,∴
,∴ ![]() =
= ![]() ,
, ![]() ,
,
∵S△AOB关于μ在[ ![]() ,2]单调递增,
,2]单调递增,
∴ ![]() ,∴△AOB的面积的取值范围是[
,∴△AOB的面积的取值范围是[ ![]() ,
, ![]() ]
]
【解析】本题主要考查圆锥曲线的综合应用和平面向量的数量积的问题。第一小题主要考查圆锥曲线的轨迹方程的问题,根据已知条件中的垂直平分线,根据垂直平分线的特点,可以得到动点到两定点的和为定值,可以得出轨迹为椭圆,根据椭圆的特点确定a,b,c即可。第二小题主要考查直线与圆锥曲线的综合应用的问题,要求三角形的面积,就要先找到底和高,由已知条件可知,高是确定的1,所以求底也就是要求弦长的问题,也就要联立直线和椭圆方程,然后利用韦达定理和向量的数量积进行求解弦长AB即可。


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:
【题目】在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )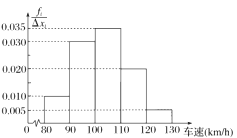
A.30辆
B.1700辆
C.170辆
D.300辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线 ![]() 的焦点,斜率为
的焦点,斜率为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() ,
, ![]() (
( ![]() )两点,且
)两点,且 ![]() .
.
(1)求该抛物线的方程;
(2)![]() 为坐标原点,
为坐标原点, ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了![]() 场比赛,比赛得分情况如下(单位:分)
场比赛,比赛得分情况如下(单位:分)
甲:![]()
乙:![]()

(1)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(2)设甲篮球运动员![]() 场比赛得分平均值
场比赛得分平均值![]() ,将
,将![]() 场比赛得分
场比赛得分![]() 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义;
的统计学意义;
(3)如果从甲、乙两位运动员的![]() 场得分中,各随机抽取一场不少于
场得分中,各随机抽取一场不少于![]() 分的得分,求甲的得分大于乙的得分的概率.
分的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某淘宝商城在2017年前7个月的销售额![]() (单位:万元)的数据如下表,已知
(单位:万元)的数据如下表,已知![]() 与
与![]() 具有较好的线性关系.
具有较好的线性关系. 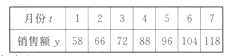
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)分析该淘宝商城2017年前7个月的销售额的变化情况,并预测该商城8月份的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
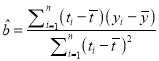 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]()
(1) 证明:数列![]() 是等比数列;
是等比数列;
(2) 求使不等式![]() 成立的所有正整数m、n的值;
成立的所有正整数m、n的值;
(3) 如果常数0 < t < 3,对于任意的正整数k,都有![]() 成立,求t的取值范围.
成立,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com