
【题目】如图,已知正方体![]() 的棱长为1.
的棱长为1.
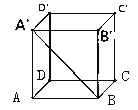
![]() 正方体
正方体![]() 中哪些棱所在的直线与直线
中哪些棱所在的直线与直线![]() 是异面直线?
是异面直线?
![]() 若M,N分别是
若M,N分别是![]() ,
,![]() 的中点,求异面直线MN与BC所成角的大小.
的中点,求异面直线MN与BC所成角的大小.
科目:高中数学 来源: 题型:
【题目】已知点![]() 和非零实数
和非零实数![]() ,若两条不同的直线
,若两条不同的直线![]() 、
、![]() 均过点
均过点![]() ,且斜率之积为
,且斜率之积为![]() ,则称直线
,则称直线![]() 、
、![]() 是一组“
是一组“![]() 共轭线对”,如直线
共轭线对”,如直线![]() 和
和![]() 是一组“
是一组“![]() 共轭线对”,其中
共轭线对”,其中![]() 是坐标原点.
是坐标原点.

(1)已知![]() 、
、![]() 是一组“
是一组“![]() 共轭线对”,且知直线
共轭线对”,且知直线![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)如图,已知点![]() 、点
、点![]() 和点
和点![]() 分别是三条倾斜角为锐角的直线
分别是三条倾斜角为锐角的直线![]() 、
、![]() 、
、![]() 上的点(
上的点(![]() 、
、![]() 、
、![]() 与
与![]() 、
、![]() 、
、![]() 均不重合),且直线
均不重合),且直线![]() 、
、![]() 是“
是“![]() 共轭线对”,直线
共轭线对”,直线![]() 、
、![]() 是“
是“![]() 共轭线对”,直线
共轭线对”,直线![]() 、
、![]() 是“
是“![]() 共轭线对”,求点
共轭线对”,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,直线
,直线![]() 、
、![]() 是“
是“![]() 共轭线对”,当
共轭线对”,当![]() 的斜率变化时,求原点
的斜率变化时,求原点![]() 到直线
到直线![]() 、
、![]() 的距离之积的取值范围.
的距离之积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店为迎接端午节,推出两款粽子:花生粽和肉粽.为调查这两款粽子的受欢迎程度,店员连续10天记录了这两种粽子的销售量,如下表表示(其中销售单位:个)
天数 销售量
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
花生粽 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 | 100 |
肉粽 | 88 | 97 | 98 | 95 | 101 | 98 | 103 | 106 | 103 | 111 | 100 |
(1)根据两组数据完成下面茎叶图:
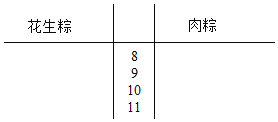
(2)统计学知识,请评述哪款粽子更受欢迎;
(3)求肉粽销售量y关于天数t的线性回归方程,并预估第15天肉粽的销售量(回归方程系数精确到0.1)
参考数据:![]() ,参考公式:
,参考公式: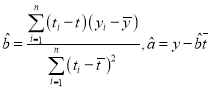
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,侧棱
是直角梯形,侧棱![]() 底面
底面![]() ,
,![]() 垂直于
垂直于![]() 和
和![]() ,
,![]() 为棱
为棱![]() 上的点,
上的点,![]() .
.

(1)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)当![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是
(1)命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
(2)l为直线,![]() ,
,![]() 为两个不同的平面,若
为两个不同的平面,若![]() ,
,![]() ,则
,则![]() ;
;
(3)给定命题p,q,若“![]() 为真命题”,则
为真命题”,则![]() 是假命题;
是假命题;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. (1)(4)B. (2)(3)C. (3)(4)D. (1)(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,双曲线![]() :
:![]() 经过点
经过点![]() ,其中一条近线的方程为
,其中一条近线的方程为![]() ,椭圆
,椭圆![]() :
:![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 椭圆
椭圆![]() 的左焦点,左顶点和上顶点分别为F,A,B,且点F到直线AB的距离为
的左焦点,左顶点和上顶点分别为F,A,B,且点F到直线AB的距离为![]() .
.
![]() 求双曲线
求双曲线![]() 的方程;
的方程;
![]() 求椭圆
求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,数轴x、y的交点为O,夹角为![]() ,与x轴、y轴正向同向的单位向量分别是
,与x轴、y轴正向同向的单位向量分别是![]() ,
,![]() ,由平面向量基本定理,对于平面内的任一向量,存在唯一的有序实数对
,由平面向量基本定理,对于平面内的任一向量,存在唯一的有序实数对![]() ,使得
,使得![]() ,我们把
,我们把![]() 叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标)
叫做点P在斜坐标系xOy中的坐标(以下各点的坐标都指在斜坐标系xOy中的坐标)
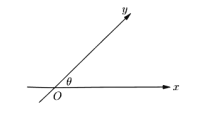
(1)若![]() ,
,![]() 为单位向量,且
为单位向量,且![]() 与
与![]() 的夹角为120°,求点P的坐标;
的夹角为120°,求点P的坐标;
(2)若![]() ,点P的坐标为
,点P的坐标为![]() ,求向量
,求向量![]() 与
与![]() 的夹角;
的夹角;
(3)若![]() ,直线l经过点
,直线l经过点![]() ,求原点O到直线l的距离的最大值.
,求原点O到直线l的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com