
【题目】已知四棱锥![]() 的底面
的底面![]() 是矩形,
是矩形,![]() 底面
底面![]() ,且
,且![]() ,设E、F、G分别为PC、BC、CD的中点,H为EG的中点,如图.
,设E、F、G分别为PC、BC、CD的中点,H为EG的中点,如图.
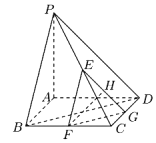
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线FH与平面![]() 所成角的大小.
所成角的大小.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是2020项的实数数列,
是2020项的实数数列,![]() 中的每一项都不为零,
中的每一项都不为零,![]() 中任意连续11项
中任意连续11项![]() 的乘积是定值
的乘积是定值![]() .
.
①存在满足条件的数列,使得其中恰有365个1;
②不存在满足条件的数列,使得其中恰有550个1.
命题的真假情况为( )
A.①和②都是真命题B.①是真命题,②是假命题
C.②是真命题,①是假命题D.①和②都是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
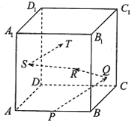
【题目】如图,在正方体![]() 中,棱
中,棱![]() 的中点为
的中点为![]() ,若光线从点
,若光线从点![]() 出发,依次经三个侧面
出发,依次经三个侧面![]() ,
,![]() ,
,![]() 反射后,落到侧面
反射后,落到侧面![]() (不包括边界),则入射光线
(不包括边界),则入射光线![]() 与侧面
与侧面![]() 所成角的正切值的范围是( )
所成角的正切值的范围是( )
A.![]() B.
B.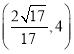 C.
C. D.
D.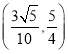
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“勾股定理”在西方被称为“毕达哥拉斯定理”,国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明![]() 如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形
如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个大正方形![]() 若直角三角形中较小的锐角
若直角三角形中较小的锐角![]() ,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是
,现在向该大止方形区域内随机地投掷一枚飞镖,则飞镖落在阴影部分的概率是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.

(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:
有下述四个结论:
①函数![]() 在其定义域上为增函数;
在其定义域上为增函数;
②对于任意的![]() ,都有
,都有![]() 成立;
成立;
③![]() 有且仅有两个零点;
有且仅有两个零点;
④若![]() 在点
在点![]() 处的切线也是
处的切线也是![]() 的切线,则
的切线,则![]() 必是
必是![]() 零点.
零点.
其中所有正确的结论序号是( )
A.①②③B.①②C.②③④D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线被椭圆截得的线段长为
轴垂直的直线被椭圆截得的线段长为![]() ,且
,且![]() 与短轴两端点的连线相互垂直.
与短轴两端点的连线相互垂直.
(1)求椭圆![]() 的方程;
的方程;
(2)若圆![]() 上存在两点
上存在两点![]() ,
,![]() ,椭圆
,椭圆![]() 上存在两个点
上存在两个点![]() 满足:
满足:![]() 三点共线,
三点共线,![]() 三点共线,且
三点共线,且![]() ,求四边形
,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车又称为小黄车,近年来逐渐走进了人们的生活,也成为减少空气污染,缓解城市交通压力的一种重要手段.为调查某地区居民对共享单车的使用情况,从该地区居民中按年龄用随机抽样的方式随机抽取了![]() 人进行问卷调查,得到这
人进行问卷调查,得到这![]() 人对共享单车的评价得分统计填入茎叶图,如下所示(满分
人对共享单车的评价得分统计填入茎叶图,如下所示(满分![]() 分):
分):

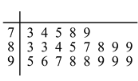
(1)找出居民问卷得分的众数和中位数;
(2)请计算这![]() 位居民问卷的平均得分;
位居民问卷的平均得分;
(3)若在成绩为![]() 分的居民中随机抽取
分的居民中随机抽取![]() 人,求恰有
人,求恰有![]() 人成绩超过
人成绩超过![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
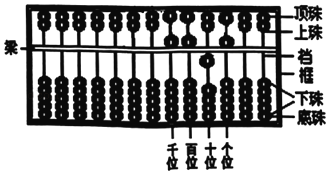
【题目】珠算被誉为中国的第五大发明,最早见于汉朝徐岳撰写的《数术记遗》2013年联合国教科文组织正式将中国珠算项目列入教科文组织人类非物质文化遗产.如图,我国传统算盘每一档为两粒上珠,五粒下珠,也称为“七珠算盘”.未记数(或表示零)时,每档的各珠位置均与图中最左档一样;记数时,要拨珠靠梁,一个上珠表示“5”,一个下珠表示“1”,例如:当千位档一个上珠、百位档一个上珠、十位档一个下珠、个位档一个上珠分别靠梁时,所表示的数是5515.现选定“个位档”、“十位档”、“百位档”和“千位档”,若规定每档拨动一珠靠梁(其它各珠不动),则在其可能表示的所有四位数中随机取一个数,这个数能被3整除的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com