
ΓΨΧβΡΩΓΩΈΣΝΥ¥ρΜςΚΘΒΝΖΗΉοΘ§ΦΉΓΔ““ΓΔ±ϊ»ΐΙζΚΘΨϋΫχ––ΝΣΚœΨϋ ¬―ίœΑΘ§Ζ÷±π≈…≥ω“ΜΥ“ΨϋΫΔAΘ§BΘ§C.―ίœΑ“Σ«σΘΚ»ΈΚΈ ±ΩΧΨϋΫΔAΓΔBΓΔCΨυ≤ΜΒΟ‘ΎΆ§“ΜΧθ÷±œΏ…œ.
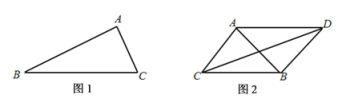
Θ®1Θ©»γΆΦ1Θ§»τ―ίœΑΙΐ≥Χ÷–Θ§AΓΔBΦδΒΡΨύάκ Φ÷’±Θ≥÷![]() Θ§BΘ§CΦδΒΡΨύάκ Φ÷’±Θ≥÷
Θ§BΘ§CΦδΒΡΨύάκ Φ÷’±Θ≥÷![]() Θ§«σ
Θ§«σ![]() ΒΡΉν¥σ÷Β.
ΒΡΉν¥σ÷Β.
Θ®2Θ©»γΆΦ2Θ§»τ―ίœΑΙΐ≥Χ÷–Θ§AΘ§CΦδΒΡΨύάκ Φ÷’±Θ≥÷![]() Θ§BΓΔCΦδΒΡΨύάκ Φ÷’±Θ≥÷
Θ§BΓΔCΦδΒΡΨύάκ Φ÷’±Θ≥÷![]() .«“Β±
.«“Β±![]() ±δΜ· ±Θ§ΡΘΡβΚΘΒΝ¥§D Φ÷’±Θ≥÷ΘΚΒΫBΒΡΨύάκ”κAΓΔBΦδΒΡΨύάκœύΒ»Θ§
±δΜ· ±Θ§ΡΘΡβΚΘΒΝ¥§D Φ÷’±Θ≥÷ΘΚΒΫBΒΡΨύάκ”κAΓΔBΦδΒΡΨύάκœύΒ»Θ§![]() Θ§”κC‘Ύ÷±œΏABΒΡΝΫ≤ύΘ§«σC”κDΦδΒΡΉν¥σΨύάκ.
Θ§”κC‘Ύ÷±œΏABΒΡΝΫ≤ύΘ§«σC”κDΦδΒΡΉν¥σΨύάκ.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®2Θ©C”κDΦδΒΡΉν¥σΨύάκΈΣ
Θ®2Θ©C”κDΦδΒΡΉν¥σΨύάκΈΣ![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©”…’ΐœ“Ε®άμ«σ≥ω![]() ΒΡ»Γ÷ΒΖΕΈßΚσΩ…ΒΟ
ΒΡ»Γ÷ΒΖΕΈßΚσΩ…ΒΟ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
Θ®2Θ©Θ©“‘CΈΣΉχ±ξ‘≠ΒψΘ§CBΥυ‘Ύ÷±œΏΈΣx÷αΘ§Ϋ®ΝΔ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOyΘ§
‘ρ![]() Θ§”…
Θ§”…![]() Θ§ΒΟA‘Ύ‘≤
Θ§ΒΟA‘Ύ‘≤![]() …œ.…η
…œ.…η![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§”…ΒΫ
Θ§”…ΒΫ![]() ΦΑ
ΦΑ![]() Θ§”κC‘Ύ÷±œΏABΒΡΝΫ≤ύΘ§Ω…
Θ§”κC‘Ύ÷±œΏABΒΡΝΫ≤ύΘ§Ω…![]() Θ§¥”ΕχΒΟ
Θ§¥”ΕχΒΟ![]() ΒψΉχ±ξΘ§¥ζ»κ
ΒψΉχ±ξΘ§¥ζ»κ![]() ΒψΙλΦΘΖΫ≥ΧΩ…ΒΟ
ΒψΙλΦΘΖΫ≥ΧΩ…ΒΟ![]() ΒψΙλΦΘΖΫ≥ΧΘ§÷ΣΙλΦΘΈΣ‘≤Θ§¥”Εχ”…Βψ”κ‘≤ΒΡΈΜ÷ΟΙΊœΒΩ…ΒΟΉν¥σΨύάκΘ°
ΒψΙλΦΘΖΫ≥ΧΘ§÷ΣΙλΦΘΈΣ‘≤Θ§¥”Εχ”…Βψ”κ‘≤ΒΡΈΜ÷ΟΙΊœΒΩ…ΒΟΉν¥σΨύάκΘ°
“ρΈΣ»ΈΚΈ ±ΩΧΨϋΫΔAΘ§BΘ§CΨυ≤ΜΒΟ‘ΎΆ§“ΜΧθ÷±œΏ…œΘ§Υυ“‘ΙΙ≥…![]() Θ§Φ«Ϋ«AΘ§BΘ§CΒΡΕ‘±ΏΖ÷±πΈΣaΘ§bΘ§c.
Θ§Φ«Ϋ«AΘ§BΘ§CΒΡΕ‘±ΏΖ÷±πΈΣaΘ§bΘ§c.
Θ®1Θ©‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§
”…’ΐœ“Ε®άμ![]() Θ§ΒΟ
Θ§ΒΟ![]()
Υυ“‘![]() .
.
”÷“ρΈΣ![]() .Υυ“‘
.Υυ“‘![]()
¥πΘΚΓœACBΒΡΉν¥σ÷Β «![]() .
.
Θ®2Θ©“‘CΈΣΉχ±ξ‘≠ΒψΘ§CBΥυ‘Ύ÷±œΏΈΣx÷αΘ§Ϋ®ΝΔ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOyΘ§
‘ρ![]()

“ρΈΣ![]() Θ§Υυ“‘A‘Ύ‘≤
Θ§Υυ“‘A‘Ύ‘≤![]() …œ.
…œ.
…η![]() Θ§‘ρ
Θ§‘ρ![]() .
.
“ρΈΣD Φ÷’±Θ≥÷ΘΚΒΫBΒΡΨύάκ”κAΘ§BΦδΒΡΨύάκœύΒ»Θ§
«“![]() Θ§”κC‘Ύ÷±œΏABΒΡΝΫ≤ύΘ§
Θ§”κC‘Ύ÷±œΏABΒΡΝΫ≤ύΘ§
Υυ“‘![]() Θ§Υυ“‘
Θ§Υυ“‘![]() .
.
¥ζ»κΖΫ≥Χ![]() ÷–Θ§ΒΟ
÷–Θ§ΒΟ![]() Θ§
Θ§
Υυ“‘D‘Ύ“‘Βψ![]() ΈΣ‘≤–Ρ1ΈΣΑκΨΕΒΡ‘≤…œΘ§
ΈΣ‘≤–Ρ1ΈΣΑκΨΕΒΡ‘≤…œΘ§
Ι ![]() .
.
¥πΘΚC”κDΦδΒΡΉν¥σΨύάκΈΣ![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§«“
Θ§«“![]() ΒΡΉν–Γ÷ΒΈΣ
ΒΡΉν–Γ÷ΒΈΣ![]() Θ°
Θ°
Θ®1Θ©«σ Β ΐ![]() ΒΡ÷ΒΦΑΚ· ΐ
ΒΡ÷ΒΦΑΚ· ΐ![]() ΒΡΒΞΒςΒίΦθ«χΦδΘΜ
ΒΡΒΞΒςΒίΦθ«χΦδΘΜ
Θ®2Θ©Β±![]() ±Θ§»τΚ· ΐ
±Θ§»τΚ· ΐ![]() ”–«“Ϋω”–“ΜΗωΝψΒψΘ§«σ Β ΐ
”–«“Ϋω”–“ΜΗωΝψΒψΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]()
Θ®1Θ©»τΚ· ΐ![]() ”–«“÷Μ”–“ΜΗωΝψΒψΘ§«σ Β ΐ
”–«“÷Μ”–“ΜΗωΝψΒψΘ§«σ Β ΐ![]() ΒΡ÷Β
ΒΡ÷Β
Θ®2Θ©»τ![]() Ε‘»Έ“β
Ε‘»Έ“β![]() Κψ≥…ΝΔΘ§«σ Β ΐ
Κψ≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß
ΒΡ»Γ÷ΒΖΕΈß
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§”…÷±»ΐάβ÷υ![]() ΚΆΥΡάβΉΕ
ΚΆΥΡάβΉΕ![]() ΙΙ≥…ΒΡΦΗΚΈΧε÷–Θ§
ΙΙ≥…ΒΡΦΗΚΈΧε÷–Θ§ ![]() Θ§ΤΫΟφ
Θ§ΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ°
Θ°
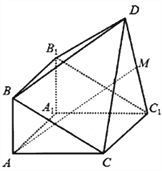
Θ®ΔώΘ©«σ÷ΛΘΚ ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©‘ΎœΏΕΈ![]() …œ «Ζώ¥φ‘ΎΒψ
…œ «Ζώ¥φ‘ΎΒψ![]() Θ§ Ι÷±œΏ
Θ§ Ι÷±œΏ![]() ”κΤΫΟφ
”κΤΫΟφ![]() Υυ≥…ΒΡΫ«ΈΣ
Υυ≥…ΒΡΫ«ΈΣ![]() ΘΩ»τ¥φ‘ΎΘ§«σ
ΘΩ»τ¥φ‘ΎΘ§«σ![]() ΒΡ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘ§»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΕύΟφΧε÷–Θ§ADΓΆΤΫΟφPDCΘ§ΥΡ±Ώ–ΈABCDΈΣΤΫ––ΥΡ±Ώ–ΈΘ§ΒψEΘ§FΖ÷±πΈΣADΘ§BPΒΡ÷–ΒψΘ§ADΘΫ3Θ§APΘΫ3![]() Θ§PC
Θ§PC![]() Θ°
Θ°
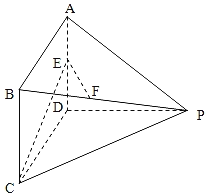
Θ®1Θ©«σ÷ΛΘΚEF//ΤΫΟφPDCΘΜ
Θ®2Θ©»τΓœCDPΘΫ120ΓψΘ§«σΕΰΟφΫ«E©¹CP©¹DΒΡΤΫΟφΫ«ΒΡ”ύœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΦ·Κœ![]() Θ§¥”P÷–»Έ»Γ2Ηω‘ΣΥΊΘ§Ζ÷±πΦ«ΈΣaΘ§b.
Θ§¥”P÷–»Έ»Γ2Ηω‘ΣΥΊΘ§Ζ÷±πΦ«ΈΣaΘ§b.
Θ®1Θ©»τ![]() Θ§ΥφΜζ±δΝΩX±μ Ψab±Μ3≥ΐΒΡ”ύ ΐΘ§«σ
Θ§ΥφΜζ±δΝΩX±μ Ψab±Μ3≥ΐΒΡ”ύ ΐΘ§«σ![]()
![]() ΒΡΗ≈¬ ΘΜ
ΒΡΗ≈¬ ΘΜ
Θ®2Θ©»τ![]() Θ®
Θ®![]() «“
«“![]() Θ©Θ§ΥφΜζ±δΝΩY±μ Ψ
Θ©Θ§ΥφΜζ±δΝΩY±μ Ψ![]() ±Μ5≥ΐΒΡ”ύ ΐΘ§«σYΒΡΗ≈¬ Ζ÷≤ΦΦΑ ΐ―ßΤΎΆϊ
±Μ5≥ΐΒΡ”ύ ΐΘ§«σYΒΡΗ≈¬ Ζ÷≤ΦΦΑ ΐ―ßΤΎΆϊ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§Τδ÷–e «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐ
Θ§Τδ÷–e «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐ
Θ®1Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡΉν–Γ÷ΒΘΜ
ΒΡΉν–Γ÷ΒΘΜ
Θ®2Θ©Φ«fΘ®xΘ©ΒΡΆΦœσ‘Ύ![]() ¥ΠΒΡ«–œΏΒΡΉίΫΊΨύΈΣ
¥ΠΒΡ«–œΏΒΡΉίΫΊΨύΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡΦΪ÷ΒΘΜ
ΒΡΦΪ÷ΒΘΜ
Θ®3Θ©»τ![]() ”–2ΗωΝψΒψ
”–2ΗωΝψΒψ![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() Θ§
Θ§![]() ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐ.
ΈΣΉ‘»ΜΕ‘ ΐΒΡΒΉ ΐ.
Θ®1Θ©Χ÷¬έ![]() ΒΡΦΪ÷ΒΘΜ
ΒΡΦΪ÷ΒΘΜ
Θ®2Θ©Β±![]() «“
«“![]() ±Θ§«σ÷ΛΘΚ
±Θ§«σ÷ΛΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΈΣ
ΒΡάκ–Ρ¬ ΈΣ![]() Θ§ΕΧ÷αΒΡ“ΜΗωΕΥΒψΒΫ”“ΫΙΒψΒΡΨύάκΈΣ2Θ°
Θ§ΕΧ÷αΒΡ“ΜΗωΕΥΒψΒΫ”“ΫΙΒψΒΡΨύάκΈΣ2Θ°

Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η![]() Ζ÷±πΈΣΆ÷‘≤
Ζ÷±πΈΣΆ÷‘≤![]() ΒΡΉσΓΔ”“ΕΞΒψΘ§»γΆΦΘ§ΙΐΒψ
ΒΡΉσΓΔ”“ΕΞΒψΘ§»γΆΦΘ§ΙΐΒψ![]() Ζ÷±πΉς÷±œΏ
Ζ÷±πΉς÷±œΏ![]() ”κ
”κ![]() Θ§…η÷±œΏ
Θ§…η÷±œΏ![]() ΫΜΆ÷‘≤
ΫΜΆ÷‘≤![]() ”ΎΝμ“ΜΒψ
”ΎΝμ“ΜΒψ![]() ΫΜΆ÷‘≤
ΫΜΆ÷‘≤![]() ”ΎΝμ“ΜΒψ
”ΎΝμ“ΜΒψ![]() Θ§Ζ÷±πΙΐ
Θ§Ζ÷±πΙΐ![]() ΚΆ
ΚΆ![]() ΉςΆ÷‘≤
ΉςΆ÷‘≤![]() ΒΡΝΫΧθ«–œΏΘ§«“ΝΫΧθ«–œΏΫΜ”ΎΒψ
ΒΡΝΫΧθ«–œΏΘ§«“ΝΫΧθ«–œΏΫΜ”ΎΒψ![]() Θ§Ζ÷±πΙΐ
Θ§Ζ÷±πΙΐ![]() ΚΆ
ΚΆ![]() ΉςΆ÷‘≤
ΉςΆ÷‘≤![]() ΒΡΝΫΧθ«–œΏΘ§«“ΝΫΧθ«–œΏΫΜ”ΎΒψ
ΒΡΝΫΧθ«–œΏΘ§«“ΝΫΧθ«–œΏΫΜ”ΎΒψ![]() Θ°÷ΛΟςΘΚΒψ
Θ°÷ΛΟςΘΚΒψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ°
…œΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com