
【题目】已知集合![]() ,从P中任取2个元素,分别记为a,b.
,从P中任取2个元素,分别记为a,b.
(1)若![]() ,随机变量X表示ab被3除的余数,求
,随机变量X表示ab被3除的余数,求![]()
![]() 的概率;
的概率;
(2)若![]() (
(![]() 且
且![]() ),随机变量Y表示
),随机变量Y表示![]() 被5除的余数,求Y的概率分布及数学期望
被5除的余数,求Y的概率分布及数学期望![]() .
.
【答案】(1)![]() (2)分布列详见解析,
(2)分布列详见解析,![]() .
.
【解析】
(1)从10个数中任取2个数有![]() 种可能,其中
种可能,其中![]() 被3除余数为0,可分为两类,一类两个数是从
被3除余数为0,可分为两类,一类两个数是从![]() 中取得,一类是一个数从
中取得,一类是一个数从![]() 中取,一个数有其余7个数中取,这样可得基本事件的个数,从而得概率.
中取,一个数有其余7个数中取,这样可得基本事件的个数,从而得概率.
(2)把集合![]() 中的数按除以5后所得余数分成5类,
中的数按除以5后所得余数分成5类,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .随机变量Y的可能取值为0,1,2,3,4,如事件“
.随机变量Y的可能取值为0,1,2,3,4,如事件“![]() ”分三类:从
”分三类:从![]() 中任取2个数,从
中任取2个数,从![]() ,
,![]() 中各取1个数,从
中各取1个数,从![]() ,
,![]() 中各取1个数,以上类推可求得各概率,得概率分布列,再由期望公式计算出期望.
中各取1个数,以上类推可求得各概率,得概率分布列,再由期望公式计算出期望.
(1)当![]() 时,从集合
时,从集合![]() 中任取2个元素a,b,共有
中任取2个元素a,b,共有![]() 种等可能基本事件,其中
种等可能基本事件,其中![]()
![]() 共包括
共包括![]() 种基本事件,
种基本事件,
所以![]() .
.
(2)当![]() 时,将集合
时,将集合![]() 中元素按被5除的余数分为五类:
中元素按被5除的余数分为五类:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
因为随机变量Y表示![]() 被5除的余数,所以Y的可能取值为0,1,2,3,4.
被5除的余数,所以Y的可能取值为0,1,2,3,4.
事件“![]() ”分三类:从
”分三类:从![]() 中任取2个数,从
中任取2个数,从![]() ,
,![]() 中各取1个数,从
中各取1个数,从![]() ,
,![]() 中各取1个数,所以
中各取1个数,所以
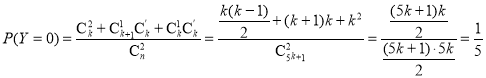
同理可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
则Y的概率分布如下:
Y | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以![]() .
.


科目:高中数学 来源: 题型:
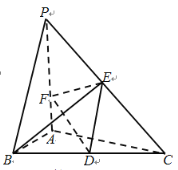
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() ,
,![]() ,
,![]() ,D,E分别为棱BC,PC的中点,点F在棱PA上,设
,D,E分别为棱BC,PC的中点,点F在棱PA上,设![]() .
.
(1)当![]() 时,求异面直线DF与BE所成角的余弦值;
时,求异面直线DF与BE所成角的余弦值;
(2)试确定t的值,使二面角C-EF-D的平面角的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为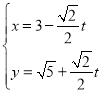 (
(![]() 为参数)。在极坐标系(与直角坐标系
为参数)。在极坐标系(与直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设圆![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 的坐标为
的坐标为![]() ,求
,求![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列两个命题,命题甲:平面α与平面β相交;命题乙:相交直线l,m都在平面α内,并且都不在平面β内,直线l,m中至少有一条与平面β相交.则甲是乙的( )
A.充分且必要条件B.充分而不必要条件
C.必要而不充分条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打击海盗犯罪,甲、乙、丙三国海军进行联合军事演习,分别派出一艘军舰A,B,C.演习要求:任何时刻军舰A、B、C均不得在同一条直线上.
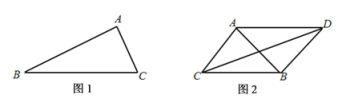
(1)如图1,若演习过程中,A、B间的距离始终保持![]() ,B,C间的距离始终保持
,B,C间的距离始终保持![]() ,求
,求![]() 的最大值.
的最大值.
(2)如图2,若演习过程中,A,C间的距离始终保持![]() ,B、C间的距离始终保持
,B、C间的距离始终保持![]() .且当
.且当![]() 变化时,模拟海盗船D始终保持:到B的距离与A、B间的距离相等,
变化时,模拟海盗船D始终保持:到B的距离与A、B间的距离相等,![]() ,与C在直线AB的两侧,求C与D间的最大距离.
,与C在直线AB的两侧,求C与D间的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提升学生“数学建模”的核心素养,某校数学兴趣活动小组指导老师给学生布置了一项探究任务:如图,有一张边长为27cm的等边三角形纸片ABC,从中裁出等边三角形纸片![]() 作为底面,从剩余梯形
作为底面,从剩余梯形![]() 中裁出三个全等的矩形作为侧面,围成一个无盖的三棱柱(不计损耗).
中裁出三个全等的矩形作为侧面,围成一个无盖的三棱柱(不计损耗).
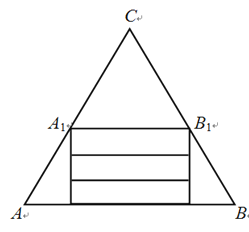
(1)若三棱柱的侧面积等于底面积,求此三棱柱的底面边长;
(2)当三棱柱的底面边长为何值时,三棱柱的体积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生了新冠肺炎疫情,2020年初开始蔓延.党中央国务院面对“突发灾难”果断采取措施,举国上下,万众一心支援武汉,全国各地医疗队陆续增援湖北,纷纷投身疫情防控与救治病人之中.为了分担“抗疫英雄”的后顾之忧,某校教师志愿者开展“爱心辅导”活动,为抗疫前线医务工作者子女开展在线辅导.春节期间随机安排甲乙两位志愿者为一位初中生辅导功课共3次,每位志愿者至少辅导1次,每一次只有1位志愿者辅导,到甲恰好辅导两次的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com