
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
![]() 当
当![]() 时,求函数
时,求函数![]() 的单调区间,并求出其极值;
的单调区间,并求出其极值;
![]() 若函数
若函数![]() 存在两个零点,求k的取值范围.
存在两个零点,求k的取值范围.
【答案】(1)单调增区间为(-∞,-1)和(0,+∞);单调减区间为(-1,0).极大值为![]() ;极小值为f(0)=0.(2)(-∞,0).
;极小值为f(0)=0.(2)(-∞,0).
【解析】
(1)先求导数,再求导函数零点,根据导函数符号变化规律,确定单调区间与极值,(2)先求导数,再结合导函数零点,根据k的值分五种情况分类讨论,结合对应函数单调性以及极值正负确定零点个数,即得结果.
解:(1)当k=1时,![]() ,
,
∴f'(x)=(x+1)ex-(x+1)=(x+1)(ex-1),
故x∈(-∞,-1)时,f′(x)>0,f(x)为增函数;
x∈(-1,0)时,f′(x)<0,f(x)为减函数;
x∈(0,+∞)时,f'(x)>0,f(x)为增函数.
故函数f(x)的单调增区间为(-∞,-1)和(0,+∞);单调减区间为(-1,0).
所以函数的极大值为![]() ;极小值为f(0)=0.
;极小值为f(0)=0.
(2)由已知,![]() ,g(x)=kex-x,
,g(x)=kex-x,
∴![]() ,
,
∴F'(x)=kxex-x=x(kex-1).
①当k<0时,F(x)在(-∞,0)为增,在(0,+∞)为减,且注意到F(0)=-k>0,函数F(x)的图象两边向下无限伸展,故此时F(x)存在两个零点,适合题意.
②当k=0时,![]() 在(-∞,0)为增,在(0,+∞)为减,且F(0)=0,故此时F(x)只有一个零点.
在(-∞,0)为增,在(0,+∞)为减,且F(0)=0,故此时F(x)只有一个零点.
③当k=1时,![]() ,故函数(-∞,+∞)为增,易知函数F(x)只有一个零点.
,故函数(-∞,+∞)为增,易知函数F(x)只有一个零点.
④当k∈(0,1)时,![]() ,F(x)在(-∞,0)为增,
,F(x)在(-∞,0)为增,![]() 为减,
为减,![]() 为增,且F(0)=-k<0易知F(x)只有一个零点.
为增,且F(0)=-k<0易知F(x)只有一个零点.
⑤当k∈(1,+∞)时,![]() ,F(x)在
,F(x)在![]() 为增,
为增,![]() 为减,(0,+∞)为增,且
为减,(0,+∞)为增,且 ,F(0)=-k<0易知F(x)只有一个零点.
,F(0)=-k<0易知F(x)只有一个零点.
综上,k的取值范围是(-∞,0).


科目:高中数学 来源: 题型:
【题目】某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长![]() (单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
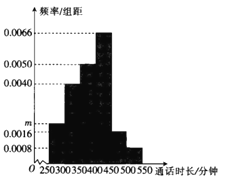
(1)求图中![]() 的值;
的值;
(2)估计该校担任班主任的教师月平均通话时长的中位数;
(3)在![]() ,
,![]() 这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实数![]() 使得
使得![]() 则称
则称![]() 是区间
是区间![]() 的
的![]() 一内点.
一内点.
(1)求证:![]() 的充要条件是存在
的充要条件是存在![]() 使得
使得![]() 是区间
是区间![]() 的
的![]() 一内点;
一内点;
(2)若实数![]() 满足:
满足:![]() 求证:存在
求证:存在![]() ,使得
,使得![]() 是区间
是区间![]() 的
的![]() 一内点;
一内点;
(3)给定实数![]() ,若对于任意区间
,若对于任意区间![]() ,
,![]() 是区间的
是区间的![]() 一内点,
一内点,![]() 是区间的
是区间的![]() 一内点,且不等式
一内点,且不等式![]() 和不等式
和不等式![]() 对于任意
对于任意![]() 都恒成立,求证:
都恒成立,求证:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 为两条不同的直线,
为两条不同的直线, ![]() ,
, ![]() 为两个不同的平面,对于下列四个命题:
为两个不同的平面,对于下列四个命题:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ②
②![]() ,
, ![]()
③![]() ,
, ![]() ,
, ![]() ④
④![]() ,
, ![]()
其中正确命题的个数有( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 在统计学中,回归分析是检验两个分类变量是否有关系的一种统计方法
B. 线性回归方程对应的直线![]() 至少经过其样本数据点中的
至少经过其样本数据点中的![]() ,
,![]() ,
,![]()
![]() 一个点
一个点
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 在回归分析中,相关指数![]() 为
为![]() 的模型比相关指数
的模型比相关指数![]() 为
为![]() 的模型拟合的效果差
的模型拟合的效果差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】禽流感一直在威胁我们的生活,某疾病控制中心为了研究禽流感病毒繁殖个数![]() (个)随时间
(个)随时间![]() (天)变化的规律,收集数据如下:
(天)变化的规律,收集数据如下:
天数 | 1 | 2 | 3 | 4 | 5 | 6 |
繁殖个数 | 6 | 12 | 25 | 49 | 95 | 190 |
作出散点图可看出样本点分布在一条指数型函数![]() 的周围.
的周围.
保留小数点后两位数的参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
(1)求出![]() 关于
关于![]() 的回归方程(保留小数点后两位数字);
的回归方程(保留小数点后两位数字);
(2)已知![]() ,估算第四天的残差.
,估算第四天的残差.
参考公式: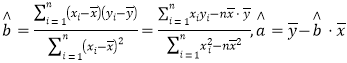
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,如果存在常数p,使得对任意正整数n,总有
,如果存在常数p,使得对任意正整数n,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“p-摆动数列”.
为“p-摆动数列”.
(Ⅰ)设![]() ,
,![]() ,
,![]() ,判断
,判断![]() 、
、![]() 是否为“p-摆动数列”,并说明理由;
是否为“p-摆动数列”,并说明理由;
(Ⅱ)已知“p-摆动数列”![]() 满足
满足![]() ,
,![]() ,求常数p的值;
,求常数p的值;
(Ⅲ)设![]() ,且数列
,且数列![]() 的前n项和为
的前n项和为![]() ,求证:数列
,求证:数列![]() 是“p-摆动数列”,并求出常数p的取值范围.
是“p-摆动数列”,并求出常数p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具公司生产甲、乙两种书柜,制柜需先制白胚再油漆,每种柜的制造白胚工时数、油漆工时数的有关数据如下:
工艺要求 | 产品甲 | 产品乙 | 生产能力(工时/天) |
制白胚工时数 | 6 | 12 | 120 |
油漆工时数 | 8 | 4 | 64 |
单位利润 | 20元 | 24元 |
则该公司合理安排这两种产品的生产,每天可获得的最大利润为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com