【题目】将函数y=sin2x（x∈R）图象上所有的点向左平移 
个单位长度，所得图象的函数解析式为 ．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，0＜φ＜ 
）的图象与x轴的交点中，相邻两个交点之间的距离为 ，且图象上一个最高点为M（ 
，3）．
（1）求f（x）的解析式；
（2）先把函数y=f（x）的图象向左平移 个单位长度，然后再把所得图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数y=g（x）的图象，试写出函数y=g（x）的解析式．
（3）在（2）的条件下，若总存在x0∈[﹣ 
， 
]，使得不等式g（x0）+2≤log3m成立，求实数m的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.
已知从全部105人中随机抽取1人为优秀的概率为
.
（1）请完成上面的列联表：若按
的可靠性要求，根据列联表的数据，能否认为“成绩与班级有关系”；
（2）若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号.试求抽到10号的概率.
附：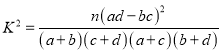 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某厂有4台大型机器，在一个月中，一台机器至多出现1次故障，且每台机器是否出现故障是相互独立的，出现故障时需1名工人进行维修，每台机器出现故障需要维修的概率为
.
(1)若出现故障的机器台数为
，求
的分布列；
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%？
(3)已知一名工人每月只有维修1台机器的能力，每月需支付给每位工人1万元的工资，每台机器不出现故障或出现故障能及时维修，就使该厂产生5万元的利润，否则将不产生利润，若该厂现有2名工人，求该厂每月获利的均值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个均匀的正方体玩具，各个面上分别写有1，2，3，4，5，6，将这个玩具先后抛掷2次，求：
（1）朝上的一面数相等的概率；
（2）朝上的一面数之和小于5的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正方体
的棱长为1， 
分别是棱
的中点，过直线
的平面分别与棱
交于
，设
, 
，给出以下四个命题：
①
②当且仅当
时，四边形
的面积最小；
③四边形
周长
, 
，则
是奇函数；
④四棱锥
的体积
为常函数；
其中正确命题的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某出租车公司响应国家节能减排的号召，已陆续购买了140辆纯电动汽车作为运营车辆，目前我国主流纯电动汽车按续航里程数
．（单位：公里）分为3类，即
类：
，
类：
， 
类：
，该公司对这140辆车的行驶总里程进行统计，结果如下表：
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
（1）从这140辆汽车中任取一辆，求该车行驶总里程超过10万公里的概率；
（2）公司为了了解这些车的工作状况，决定抽取了14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从
类车中抽取了
辆车．
①求
的值；
②如果从这
辆车中随机选取两辆车，求恰有一辆车行驶总里程超过10万公里的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（2cosωx，cos2ωx）， 
=（sinωx，1）（其中ω＞0），令f（x）= 
，且f（x）的最小正周期为π．
（1）求 
的值；
（2）写出 
上的单调递增区间．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
